二次函数 $y=\dfrac 13x^2-\dfrac 23x-1$ 的图象与 $y$ 轴交点为 $A$，过 $A$ 作直线 $l\parallel x$ 轴，将抛物线在 $y$ 轴左侧部分沿直线 $l$ 翻折，其余部分保持不变，得到一个新图象，直线 $y=\dfrac 13x+b$ 与新图象只有一个公共点 $P\left(x_0,y_0\right)$，且 $y_0\leqslant 7$，求 $b$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
当 $-1<b\leqslant 5$ 或 $b<{-\dfrac 74}$ 时，直线与新图象只有一个公共点
【解析】
如图，当 $y=\dfrac 13x+b$ 经过 $\left(0,-1\right)$ 时，与新图象有两个交点；当直线与原抛物线只有一个交点时，则与新图象有两个交点．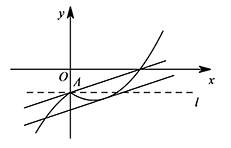
将 $\left(0,-1\right)$ 代入 $y=\dfrac 13x+b$，得 $b=-1$，
因为 $y_0\leqslant7$，所以 $\dfrac 13x^2-\dfrac 23x-1=7$ 时，
解得 $x_1=6$，$x_2=-4$．
将 $\left(6,7\right)$ 代入直线 $y=\dfrac 13x+b$，得 $b=5$，所以 $-1<b\leqslant 5$．
因为 $\dfrac 13x^2-\dfrac 23x-1=\dfrac 13x+b$，
所以 $\Delta=9+4\left(3+3b\right)=0$，即 $b=-\dfrac 74$．
综上可得，当 $-1<b\leqslant 5$ 或 $b<{-\dfrac 74}$ 时，直线与新图象只有一个公共点．
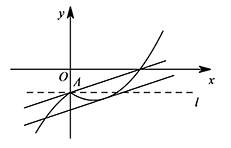将 $\left(0,-1\right)$ 代入 $y=\dfrac 13x+b$，得 $b=-1$，因为 $y_0\leqslant7$，所以 $\dfrac 13x^2-\dfrac 23x-1=7$ 时，
解得 $x_1=6$，$x_2=-4$．
将 $\left(6,7\right)$ 代入直线 $y=\dfrac 13x+b$，得 $b=5$，所以 $-1<b\leqslant 5$．
因为 $\dfrac 13x^2-\dfrac 23x-1=\dfrac 13x+b$，
所以 $\Delta=9+4\left(3+3b\right)=0$，即 $b=-\dfrac 74$．
综上可得，当 $-1<b\leqslant 5$ 或 $b<{-\dfrac 74}$ 时，直线与新图象只有一个公共点．
答案
解析
备注
