在平面直角坐标系 $xOy$ 中，点 $A$ 的坐标为 $\left(3,2\right)$，点 $B$ 的坐标为 $\left(-1,2\right)$，若抛物线 $y = a{x^2}\left(a \ne 0\right)$ 与线段 $AB$ 恰有一个公共点，结合函数的图象，求 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$a$ 的取值范围是 $\dfrac29\leqslant a<2$
【解析】
如图，当抛物线过点 $A,B$ 时为临界状态．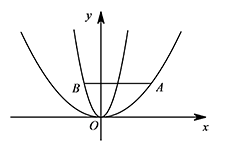
当抛物线过点 $A\left(3,2\right)$ 时，$a=\dfrac29$；
当抛物线过点 $B\left(-1,2\right)$ 时，$a=2$．
结合图象，可得满足条件的 $a$ 的取值范围是 $\dfrac29\leqslant a<2$．
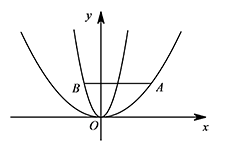当抛物线过点 $A\left(3,2\right)$ 时，$a=\dfrac29$；当抛物线过点 $B\left(-1,2\right)$ 时，$a=2$．
结合图象，可得满足条件的 $a$ 的取值范围是 $\dfrac29\leqslant a<2$．
答案
解析
备注
