已知 $\odot O$ 与 $\triangle ABC$ 的边 $AB,AC$ 分别相切于 $P,Q$，与 $\triangle ABC$ 外接圆相切于点 $D$，$M$ 是 $PQ$ 的中点（如图）．求证：$\angle POQ=2\angle MDC$．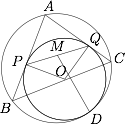
【难度】
【出处】
2008年全国高中数学联赛四川省预赛
【标注】
【答案】
略
【解析】
如图，连接 $AO,AD,DO$ 和 $DQ$．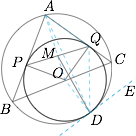
因为 $AP,AQ$ 分别于 $\odot O$ 相切于 $P,Q$，所以 $AP=AQ$．
由于 $OP$ 和 $OQ$ 都是 $\odot O$ 的半径，可知\[\angle APO=\angle AQO=90^{\circ},\]所以由对称性知 $\angle POQ=2\angle AOQ$，且 $OA\perp PQ$ 于点 $M$，因此\[OD^{2}=OQ^{2}=OM\cdot OA,\]即\[\dfrac{OD}{OM}=\dfrac{OA}{OD}.\]又因为 $\angle DOM=\angle AOD$，可知 $\triangle DOM\backsim \triangle AOD$，则 $\angle ODM=\angle OAD$．
过点 $D$ 作圆的公切线 $DE$，则 $\angle CDE=\angle CAD$．
又因为 $OD\perp DE$，即 $\angle ODE=90^{\circ}$，则\[\begin{split}\angle MDC&=90^{\circ}-\angle ODM-\angle CDE\\&=90^{\circ}-\angle OAD-\angle DAC\\&=90^{\circ}-\angle OAQ\\&=\angle AOQ,\end{split}\]故 $\angle POQ=2\angle MDC$．
因为 $AP,AQ$ 分别于 $\odot O$ 相切于 $P,Q$，所以 $AP=AQ$．由于 $OP$ 和 $OQ$ 都是 $\odot O$ 的半径，可知\[\angle APO=\angle AQO=90^{\circ},\]所以由对称性知 $\angle POQ=2\angle AOQ$，且 $OA\perp PQ$ 于点 $M$，因此\[OD^{2}=OQ^{2}=OM\cdot OA,\]即\[\dfrac{OD}{OM}=\dfrac{OA}{OD}.\]又因为 $\angle DOM=\angle AOD$，可知 $\triangle DOM\backsim \triangle AOD$，则 $\angle ODM=\angle OAD$．
过点 $D$ 作圆的公切线 $DE$，则 $\angle CDE=\angle CAD$．
又因为 $OD\perp DE$，即 $\angle ODE=90^{\circ}$，则\[\begin{split}\angle MDC&=90^{\circ}-\angle ODM-\angle CDE\\&=90^{\circ}-\angle OAD-\angle DAC\\&=90^{\circ}-\angle OAQ\\&=\angle AOQ,\end{split}\]故 $\angle POQ=2\angle MDC$．
答案
解析
备注
