在平面直角坐标系 $xOy$ 中，抛物线 $y=\dfrac 12x^2-x+2$ 与 $y$ 轴交于点 $A$，顶点为 $B$，点 $C$ 与点 $A$ 关于抛物线的对称轴对称．点 $D$ 在抛物线上，且点 $D$ 的横坐标为 $4$．将抛物线在点 $A,D$ 之间的部分（包含点 $A,D$）记为图象 $G$，若图象 $G$ 向下平移 $t\left(t>0\right)$ 个单位后与直线 $BC$ 只有一个公共点，求 $t$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$t$ 的取值范围是 $1<t\leqslant3$
【解析】
根据题意可得直线 $BC$ 的解析式为 $y=\dfrac12x+1$．
在抛物线 $y=\dfrac12x^2-x+2$ 上，当 $x=4$ 时，$y=6$，
所以点 $D$ 的坐标为 $\left(4,6\right)$．
在直线 $y=\dfrac12x-1$ 上，当 $x=0$ 时，$y=1$，当 $x=4$ 时，$y=3$．
所以点 $E$ 的坐标为 $\left(0,1\right)$，点 $F$ 的坐标为 $\left(4,3\right)$．
设点 $A$ 平移后的对应点为点 $A'$，点 $D$ 平移后的对应点为点 $D'$．
当图象 $G$ 向下平移至点 $A'$ 与点 $E$ 重合时，$t=1$；
当图象 $G$ 向下平移至点 $D'$ 与点 $F$ 重合时，$t=3$．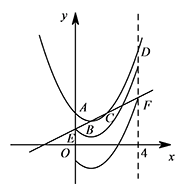
结合图象可知，符合题意的 $t$ 的取值范围是 $1<t\leqslant3$．
在抛物线 $y=\dfrac12x^2-x+2$ 上，当 $x=4$ 时，$y=6$，
所以点 $D$ 的坐标为 $\left(4,6\right)$．
在直线 $y=\dfrac12x-1$ 上，当 $x=0$ 时，$y=1$，当 $x=4$ 时，$y=3$．
所以点 $E$ 的坐标为 $\left(0,1\right)$，点 $F$ 的坐标为 $\left(4,3\right)$．
设点 $A$ 平移后的对应点为点 $A'$，点 $D$ 平移后的对应点为点 $D'$．
当图象 $G$ 向下平移至点 $A'$ 与点 $E$ 重合时，$t=1$；
当图象 $G$ 向下平移至点 $D'$ 与点 $F$ 重合时，$t=3$．
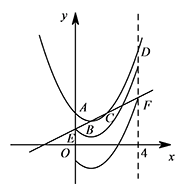结合图象可知，符合题意的 $t$ 的取值范围是 $1<t\leqslant3$．
答案
解析
备注
