题目

查看数据源：59082715060a05000980afb8

在平面直角坐标系 $xOy$ 中，对于点 $P\left(a,b\right)$ 和点 $Q\left(a,b'\right)$，给出如下定义：
若 $b'=\begin{cases}
b,&a\geqslant 1,\\
-b,&a<1,
\end{cases}$ 则称点 $Q$ 为点 $P$ 的限变点．
例如，点 $\left(2,3\right)$ 的限变点的坐标是 $\left(2,3\right)$，点 $\left(-2,5\right)$ 的限变点的坐标是 $\left(-2,-5\right)$．

【难度】

【出处】

无

【标注】

题型
>
代数部分
>
函数
>
函数与方程、不等式的关系
题型
>
代数部分
>
函数
>
函数与方程、不等式的关系

若点 $P$ 在函数 $y=-x+3$（$-2\leqslant x\leqslant k$，$k>-2$）的图象上，其限变点 $Q$ 的纵坐标 $b'$ 的取值范围是 $-5\leqslant b'\leqslant 2$，求 $k$ 的取值范围．
标注
- 题型
  >
  代数部分
  >
  函数
  >
  函数与方程、不等式的关系
答案

$k$ 的取值范围是 $5\leqslant k\leqslant 8$

解析

依题意，$y=-x+3\left(x\geqslant -2\right)$ 图象上的点 $P$ 的限变点必在函数 $y=\begin{cases}-x+3,&x\geqslant 1,\\x-3,&-2\leqslant x<1\end{cases}$ 的图象上．
如图所示，显然 $ b'\leqslant 2$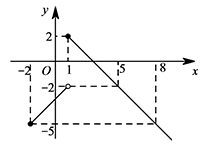．当 $x=1$ 时，$b'$ 取最大值 $2$，
当 $b'=-2$ 时，$-2=-x+3$，则 $x=5$．
当 $b'=-5$ 时，$-5=x-3$ 或 $-5=-x+3$，则 $x=-2$ 或 $x=8$．
因为 $-5\leqslant b'\leqslant 2$，结合图象，可得 $k$ 的取值范围是 $5\leqslant k\leqslant 8$．
若点 $P$ 在关于 $x$ 的二次函数 $y=x^2-2tx+t^2+t$ 的图象上，其限变点 $Q$ 的纵坐标 $b'$ 的取值范围是 $b'\geqslant m$ 或 $b'<n$，其中 $m>n$．令 $s=m-n$，求 $s$ 关于 $t$ 的函数解析式及 $s$ 的取值范围．
标注
- 题型
  >
  代数部分
  >
  函数
  >
  函数与方程、不等式的关系
答案

$s$ 的取值范围是 $s\geqslant2$

解析

因为 $y=x^2-2tx+t^2+t=\left(x-t\right)^2+t$，
所以顶点坐标为 $\left(t,t\right)$．
① 若 $t<1$，当 $x<1$ 时，点 $P$ 的纵坐标 $b$ 满足 $b\geqslant t$，则 $b'\leqslant -t$ 与题意不符．② 若 $t\geqslant 1$，当 $x\geqslant 1$ 时，点 $P$ 的纵坐标 $b$ 满足 $b\geqslant t$，则 $b'\geqslant t$，即 $m=t$；
当 $x<1$ 时，点 $P$ 的纵坐标 $b$ 满足 $b>t^2-t+1$，则 $ b'<-t^2+t-1 $，即 $n=-t^2+t-1$．所以 $s=m-n=t+t^2-t+1=t^2+1$．
所以 $s$ 关于 $t$ 的函数解析式为 $s=t^2+1$（$t\geqslant 1$）．
当 $t=1$ 时，$s$ 取最小值 $2$．
所以 $s$ 的取值范围是 $s\geqslant2$．