在平面直角坐标系 $xOy$ 中，点 $P$ 在抛物线 $y=\dfrac 12x^2-x-4$ 上，过点 $P$ 作 $y$ 轴的垂线 $l$，垂足为 $D\left(0,d\right)$．将抛物线在直线 $l$ 上方的部分沿直线 $l$ 翻折，图象的其余部分保持不变，得到一个新图象 $G$．当图象 $G$ 与直线 $y=\dfrac 12x-2$ 只有两个公共点时，求 $d$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$d$ 的取值范围为 $-\dfrac 52<d<0$
【解析】
联合抛物线方程和直线方程 $\begin{cases}y=\dfrac 12x^2-x-4,\\ y=\dfrac 12x-2,\end{cases}$
解得 $\begin{cases}x_1=-1,\\ y_1=-\dfrac 52,\end{cases}\begin{cases}x_2=4,\\ y_2=0.\end{cases}$
当 $d>0$ 时，直线 $y=\dfrac 12x-2$ 与新图象 $G$ 有 $4$ 个交点；
当 $d=0$ 时，直线 $y=\dfrac 12x-2$ 与新图象 $G$ 有 $3$ 个交点；
当 $d=-\dfrac 52$ 时，直线 $y=\dfrac 12x-2$ 与新图象 $G$ 有 $1$ 个交点．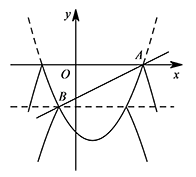
所以满足条件的 $d$ 的取值范围为 $-\dfrac 52<d<0$．
解得 $\begin{cases}x_1=-1,\\ y_1=-\dfrac 52,\end{cases}\begin{cases}x_2=4,\\ y_2=0.\end{cases}$
当 $d>0$ 时，直线 $y=\dfrac 12x-2$ 与新图象 $G$ 有 $4$ 个交点；
当 $d=0$ 时，直线 $y=\dfrac 12x-2$ 与新图象 $G$ 有 $3$ 个交点；
当 $d=-\dfrac 52$ 时，直线 $y=\dfrac 12x-2$ 与新图象 $G$ 有 $1$ 个交点．
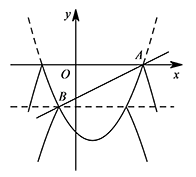所以满足条件的 $d$ 的取值范围为 $-\dfrac 52<d<0$．
答案
解析
备注
