利用光路最短原理（费马原理），证明折射定律．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $v_1,v_2$ 是光在 $AC,CB$ 路径上传播的速度，而 $\theta_1,\theta_2$ 分别是入射角和出射角的余角，则欲证明当 $\dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\cos {\theta _1}}}{{\cos {\theta _2}}}$ 时，光从 $A$ 点运动到 $B$ 点所用的时间 $\dfrac{{AC}}{{{v_1}}} + \dfrac{{BC}}{{{v_2}}}$ 最小．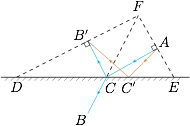
过 $B'$ 作 $CB'$ 的垂线，过 $A$ 作 $CA$ 的垂线，两条垂线交于 $F$ 点，连接 $FC$．
当 $C$ 点位于其他位置 $C'$ 时，有$$\begin{split}DF\cdot B'C'+EF\cdot AC'&>2S_{\triangle DEF}\\&=DF\cdot B'C+EF\cdot AC\\&=DF\cdot BC+EF\cdot AC,\end{split}$$于是折射定律成立．
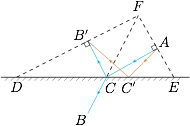过 $B'$ 作 $CB'$ 的垂线，过 $A$ 作 $CA$ 的垂线，两条垂线交于 $F$ 点，连接 $FC$．当 $C$ 点位于其他位置 $C'$ 时，有$$\begin{split}DF\cdot B'C'+EF\cdot AC'&>2S_{\triangle DEF}\\&=DF\cdot B'C+EF\cdot AC\\&=DF\cdot BC+EF\cdot AC,\end{split}$$于是折射定律成立．
答案
解析
备注
