已知椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）上两点 $A,B$ 处的切线互相垂直，且相交于点 $P$，求 $P$ 点的轨迹．
【难度】
【出处】
无
【标注】
【答案】
$x^2+y^2=a^2+b^2$
【解析】
如图，设两个切点分别 $M,N$．
作椭圆的左焦点 $F_1$ 关于两条切线 $PM,PN$ 的对称点，分别为 $F_1',F_1''$，连接 $F_1F_1',F_1F_1'',F_2F_1',F_2F_1''$，$A,B$ 分别为线段 $F_1F_1',F_1F_1''$ 的中点，连接 $OA,OB,OP$．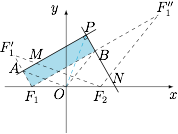
根据椭圆的光学性质，$F_2,M,F_1'$ 以及 $F_2,N,F_1''$ 均三点共线，因此$$|OA|=|OB|=a.$$由于四边形 $APBF_1$ 为矩形，因此$$|OP|^2+|OF_1|^2=|OA|^2+|OB|^2,$$即$$|OP|^2=2a^2-c^2=a^2+b^2,$$从而点 $P$ 的轨迹方程为$$x^2+y^2=a^2+b^2.$$
作椭圆的左焦点 $F_1$ 关于两条切线 $PM,PN$ 的对称点，分别为 $F_1',F_1''$，连接 $F_1F_1',F_1F_1'',F_2F_1',F_2F_1''$，$A,B$ 分别为线段 $F_1F_1',F_1F_1''$ 的中点，连接 $OA,OB,OP$．
根据椭圆的光学性质，$F_2,M,F_1'$ 以及 $F_2,N,F_1''$ 均三点共线，因此$$|OA|=|OB|=a.$$由于四边形 $APBF_1$ 为矩形，因此$$|OP|^2+|OF_1|^2=|OA|^2+|OB|^2,$$即$$|OP|^2=2a^2-c^2=a^2+b^2,$$从而点 $P$ 的轨迹方程为$$x^2+y^2=a^2+b^2.$$
答案
解析
备注
