在平面直角坐标系 $xOy$ 中，抛物线 $y=mx^2-2m^2x+2$ 交 $y$ 轴于 $A$ 点，交直线 $x=4$ 于 $B$ 点．记抛物线在 $A,B$ 之间的部分为图象 $G$（包含 $A,B$ 两点），若对于图象 $G$ 上任意一点 $P(x_P,y_P)$，始终满足 $y_P\leqslant 2$，求 $m$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$m$ 的取值范围为 $m<0$ 或 $m\geqslant 2$
【解析】
抛物线 $y=mx^2-2m^2x+2$ 的对称轴为 $x=-\dfrac{-2m^2}{2m}=m$．
① 当 $m>0$ 时，如图所示．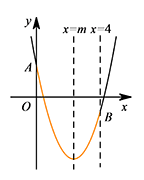
要使 $0\leqslant x\leqslant 4$ 时，始终有 $y\leqslant 2$，
只需抛物线的对称轴与直线 $x=2$ 重合或者在直线 $x=2$ 的右侧，
即 $m\geqslant 2$；
② 当 $m<0$ 时，如图所示．
此时 $0\leqslant x\leqslant 4$ 时，$y\leqslant 2$ 恒成立．
综上可得，满足题意的 $m$ 的取值范围为 $m<0$ 或 $m\geqslant 2$．
① 当 $m>0$ 时，如图所示．
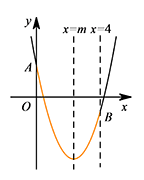要使 $0\leqslant x\leqslant 4$ 时，始终有 $y\leqslant 2$，只需抛物线的对称轴与直线 $x=2$ 重合或者在直线 $x=2$ 的右侧，
即 $m\geqslant 2$；
② 当 $m<0$ 时，如图所示．
此时 $0\leqslant x\leqslant 4$ 时，$y\leqslant 2$ 恒成立．综上可得，满足题意的 $m$ 的取值范围为 $m<0$ 或 $m\geqslant 2$．
答案
解析
备注
