已知 ${F_1} , {F_2}$ 是椭圆 $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ 的焦点．设 $l$ 是该椭圆的一条切线，${H_1} , {H_2}$ 分别是 ${F_1} , {F_2}$ 在 $l$ 上的垂足，证明：${F_1}{H_1} \cdot {F_2}{H_2} = {b^2}$．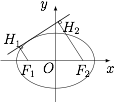
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图，连接 ${F_1}T,{F_2}T$，设 $\angle {F_1}T{F_2} = \theta $，${F_1}T = m$，${F_2}T = n$．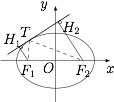
根据题意，有$$\begin{split}{F_1}H \cdot {F_2}H &= {\sin ^2}\dfrac{{{\rm{\pi }} - \theta }}{2} \cdot mn \\&= \dfrac{{1 + \cos \theta }}{2} \cdot mn \\&= \dfrac{{1 + \dfrac{{{m^2} + {n^2} - 4{c^2}}}{{2mn}}}}{2} \cdot mn \\&= \dfrac{{{{\left( {m + n} \right)}^2} - 4{c^2}}}{4} \\&= {b^2},\end{split}$$于是原命题得证．
根据题意，有$$\begin{split}{F_1}H \cdot {F_2}H &= {\sin ^2}\dfrac{{{\rm{\pi }} - \theta }}{2} \cdot mn \\&= \dfrac{{1 + \cos \theta }}{2} \cdot mn \\&= \dfrac{{1 + \dfrac{{{m^2} + {n^2} - 4{c^2}}}{{2mn}}}}{2} \cdot mn \\&= \dfrac{{{{\left( {m + n} \right)}^2} - 4{c^2}}}{4} \\&= {b^2},\end{split}$$于是原命题得证．
答案
解析
备注
