已知 $P$ 是圆 $(x-2)^2+(y-2)^2=1$ 上一动点,向量 $\overrightarrow{OP}$ 依逆时钟方向旋转 $90^{\circ}$ 得到向量 $\overrightarrow{OS}$,又点 $P$ 关于 $A(3,0)$ 的对称点为 $T$,求 $\left|\overrightarrow{TS}\right|$ 的取值范围.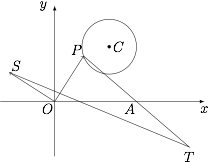

【难度】
【出处】
2009年全国高中数学联赛新疆维吾尔自治区预赛
【标注】
【答案】
$\left[\sqrt 2 (\sqrt{26}-1),\sqrt 2 (\sqrt{26}+1)\right]$
【解析】
设点 $P(x,y)$,则点 $S(-y,x)$,点 $T(6-x,-y)$.
因为圆心为 $C(2,2)$,半径 $r=1$,所以\[\begin{split}\left|\overrightarrow{TS}\right|&=\sqrt{(6-x+y)^2+(-y-x)^2}\\&=\sqrt{2x^2+2y^2-12x+12y+36}\\&=\sqrt 2 \cdot \sqrt{(x-3)^2+(y+3)^2}\\&=\sqrt 2|PB|,\end{split}\]其中点 $B(3,-3)$,
所以\[\begin{split}&\left|\overrightarrow{TS}\right|_{\max}=\sqrt 2(|CB|+1)=\sqrt 2\left(\sqrt{26}+1\right),\\ &\left|\overrightarrow{TS}\right|_{\min}=\sqrt 2(|CB|-1)=\sqrt 2\left(\sqrt{26}-1\right),\end{split}\]故$$\sqrt 2\left(\sqrt{26}-1\right)\leqslant \left|\overrightarrow{TS}\right|\leqslant \sqrt 2\left(\sqrt{26}+1\right).$$
因为圆心为 $C(2,2)$,半径 $r=1$,所以\[\begin{split}\left|\overrightarrow{TS}\right|&=\sqrt{(6-x+y)^2+(-y-x)^2}\\&=\sqrt{2x^2+2y^2-12x+12y+36}\\&=\sqrt 2 \cdot \sqrt{(x-3)^2+(y+3)^2}\\&=\sqrt 2|PB|,\end{split}\]其中点 $B(3,-3)$,
所以\[\begin{split}&\left|\overrightarrow{TS}\right|_{\max}=\sqrt 2(|CB|+1)=\sqrt 2\left(\sqrt{26}+1\right),\\ &\left|\overrightarrow{TS}\right|_{\min}=\sqrt 2(|CB|-1)=\sqrt 2\left(\sqrt{26}-1\right),\end{split}\]故$$\sqrt 2\left(\sqrt{26}-1\right)\leqslant \left|\overrightarrow{TS}\right|\leqslant \sqrt 2\left(\sqrt{26}+1\right).$$
答案
解析
备注