已知锐角 $\triangle ABC$ 中，$\angle B=60^\circ$，$P$ 为 $AB$ 中点，$Q$ 为外接圆上弧 $AC$（不包含点 $B$）的中点，$H$ 为 $\triangle ABC$ 的垂心．如果 $P,H,Q$ 三点共线，求 $\angle A$．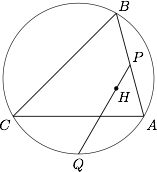
【难度】
【出处】
无
【标注】
【答案】
$75^\circ$
【解析】
如图，设 $O$ 为外接圆圆心，延长 $CO$ 交外接圆于 $D$，则四边形 $BHAD$ 为平行四边形，因此 $D,P,H$ 三点共线，进而 $D,P,H,Q$ 四点共线．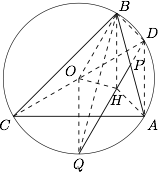
连接 $OH,BQ$，由 $\angle B=60^\circ$，于是$$BH=AD=\dfrac 12CD=OQ,$$又 $OB=OQ$，因此 $BHQO$ 为菱形，从而$$\angle OBC=\angle OCB=\angle BAD=\angle HBA,$$又$$\angle BCD=\angle BQD=\angle OBQ=\angle HBQ,$$因此 $BO,BQ,BH$ 将 $\angle CBA$ 四等分，进而不难得知 $\angle A=75^\circ$．
连接 $OH,BQ$，由 $\angle B=60^\circ$，于是$$BH=AD=\dfrac 12CD=OQ,$$又 $OB=OQ$，因此 $BHQO$ 为菱形，从而$$\angle OBC=\angle OCB=\angle BAD=\angle HBA,$$又$$\angle BCD=\angle BQD=\angle OBQ=\angle HBQ,$$因此 $BO,BQ,BH$ 将 $\angle CBA$ 四等分，进而不难得知 $\angle A=75^\circ$．
答案
解析
备注
