设 $A,B,C,D,X$ 为圆周上依次排列的五个点，已知 $\angle AXB = \angle BXC = \angle CXD$，$AX = a$，$BX = b$，$CX = c$，求 $DX$ 的长．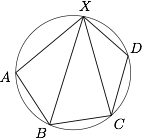
【难度】
【出处】
2015年北京大学化学体验营数学试题
【标注】
【答案】
$\dfrac{c^2+ac-b^2}{b}$
【解析】
连接 $AC$，$BD$，如图．
设 $AB=BC=CD=m$，$AC=BD=n$，则由 $A,B,C,X$ 四点共圆，由托勒密定理可得$$am+cm=bn,$$由 $B,C,D,X$ 四点共圆，由托勒密定理可得$$bm+dm=cn,$$两式相除即得 $d=\dfrac{c^2+ac-b^2}{b}$．
设 $AB=BC=CD=m$，$AC=BD=n$，则由 $A,B,C,X$ 四点共圆，由托勒密定理可得$$am+cm=bn,$$由 $B,C,D,X$ 四点共圆，由托勒密定理可得$$bm+dm=cn,$$两式相除即得 $d=\dfrac{c^2+ac-b^2}{b}$．
答案
解析
备注
