设点 $O$ 为椭圆的中心,点 $A$ 为椭圆上异于顶点的任意一点,过点 $A$ 作长轴的垂线,垂足为 $M$,连接 $AO$ 并延长交椭圆于另一点 $B$,连接 $BM$ 并延长交椭圆于点 $C$,问是否存在椭圆,使得 $BA\perp CA$?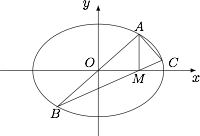

【难度】
【出处】
2014年全国高中数学联赛山东省预赛
【标注】
【答案】
存在
【解析】
以椭圆的中心为坐标原点,长轴为 $x$ 轴,建立坐标系,设椭圆方程为 $\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1$,若 $a^2=2b^2$,则必有 $BA\perp CA$.
设 $A(x_0,y_0)$,$C(x_1,y_1)$,则由题意知 $M(x_0,0)$,$B(-x_0,-y_0)$,且直线 $BC$ 的斜率一定存在,设为 $k$,则直线 $BC$ 的方程为$$y=k(x-x_0),$$代入椭圆方程并整理得$$(a^2k^2+b^2)x^2-2a^2k^2x_0x +a^2k^2x_0^2-a^2b^2=0,$$由韦达定理得:$$x_1-x_0=\dfrac {2a^2k^2x_0}{a^2k^2+b^2}.$$因此由直线 $BC$ 的方程为 $y=k(x-x_0)$ 得$$y_1=k(x_1-x_0)=k\dfrac {2a^2k^2x_0}{a^2k^2+b^2}=\dfrac {2a^2k^3x_0}{a^2k^2+b^2}.$$由题意直线 $AB$ 的斜率为$$k_{AB}=\dfrac {y_0}{x_0},$$直线 $AC$ 的斜率为$$k_{AC}=\dfrac {y_1-y_0}{x_1-x_0}=\dfrac {\dfrac {2a^2k^3x_0}{a^2k^2+b^2}-y_0}{\dfrac {2a^2k^2x_0}{a^2k^2+b^2}}.$$由 $BA \perp CA$ 得$$k_{AB}k_{AC}=-1.$$注意到 $k=\dfrac {y_0}{2x_0}$,整理得 $a^2=2b^2$.
设 $A(x_0,y_0)$,$C(x_1,y_1)$,则由题意知 $M(x_0,0)$,$B(-x_0,-y_0)$,且直线 $BC$ 的斜率一定存在,设为 $k$,则直线 $BC$ 的方程为$$y=k(x-x_0),$$代入椭圆方程并整理得$$(a^2k^2+b^2)x^2-2a^2k^2x_0x +a^2k^2x_0^2-a^2b^2=0,$$由韦达定理得:$$x_1-x_0=\dfrac {2a^2k^2x_0}{a^2k^2+b^2}.$$因此由直线 $BC$ 的方程为 $y=k(x-x_0)$ 得$$y_1=k(x_1-x_0)=k\dfrac {2a^2k^2x_0}{a^2k^2+b^2}=\dfrac {2a^2k^3x_0}{a^2k^2+b^2}.$$由题意直线 $AB$ 的斜率为$$k_{AB}=\dfrac {y_0}{x_0},$$直线 $AC$ 的斜率为$$k_{AC}=\dfrac {y_1-y_0}{x_1-x_0}=\dfrac {\dfrac {2a^2k^3x_0}{a^2k^2+b^2}-y_0}{\dfrac {2a^2k^2x_0}{a^2k^2+b^2}}.$$由 $BA \perp CA$ 得$$k_{AB}k_{AC}=-1.$$注意到 $k=\dfrac {y_0}{2x_0}$,整理得 $a^2=2b^2$.
答案
解析
备注