已知 $M,N$ 是椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的长轴上的两个定点,椭圆的弦 $AB$ 恒过点 $M$,直线 $AN,BN$ 分别与椭圆 $E$ 交于不同于 $A,B$ 的点 $C,D$,求证:直线 $CD$ 的斜率与直线 $AB$ 的斜率之比为定值.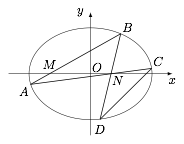

【难度】
【出处】
无
【标注】
【答案】
定值为 $\dfrac{a^2+n^2-2mn}{a^2-n^2}$
【解析】
设直线 $AB,AC,BD,CD$ 的方程分别为\[\begin{split}AB&:x-m-ty=0,\\
AC&:x-n-t_1y=0,\\
BD&:x-n-t_2y=0, \\
CD&:Ax+By+C=0,\end{split}\]过 $A,B,C,D$ 的交点曲线系为\[(x-n-t_1y)(x-n-t_2y)+\lambda\left(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}-1\right)=0,\]对比曲线 $AB\cup CD$ 的方程\[(x-m-ty)(Ax+By+C)=0,\]可得\[\begin{cases}
1+\dfrac{\lambda}{a^2}=A,\\
t_1t_2+\dfrac{\lambda}{b^2}=-Bt,\\
-(t_1+t_2)=-At+B,\\
-2n=C-mA,\\
n(t_1+t_2)=-Ct-mB,\\
n^2-\lambda=-mC,
\end{cases}\]由第一、四、六个方程可解得\[A=\dfrac{a^2+n^2-2mn}{a^2-m^2},C=\dfrac{mn^2+ma^2-2na^2}{a^2-m^2},\]根据第三、五个方程,可得直线 $CD$ 与 $AB$ 斜率之比\[-\dfrac{At}{B}=\dfrac{(m-n)A}{C+nA}=\dfrac{a^2+n^2-2mn}{a^2-n^2},\]于是原命题得证.
AC&:x-n-t_1y=0,\\
BD&:x-n-t_2y=0, \\
CD&:Ax+By+C=0,\end{split}\]过 $A,B,C,D$ 的交点曲线系为\[(x-n-t_1y)(x-n-t_2y)+\lambda\left(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}-1\right)=0,\]对比曲线 $AB\cup CD$ 的方程\[(x-m-ty)(Ax+By+C)=0,\]可得\[\begin{cases}
1+\dfrac{\lambda}{a^2}=A,\\
t_1t_2+\dfrac{\lambda}{b^2}=-Bt,\\
-(t_1+t_2)=-At+B,\\
-2n=C-mA,\\
n(t_1+t_2)=-Ct-mB,\\
n^2-\lambda=-mC,
\end{cases}\]由第一、四、六个方程可解得\[A=\dfrac{a^2+n^2-2mn}{a^2-m^2},C=\dfrac{mn^2+ma^2-2na^2}{a^2-m^2},\]根据第三、五个方程,可得直线 $CD$ 与 $AB$ 斜率之比\[-\dfrac{At}{B}=\dfrac{(m-n)A}{C+nA}=\dfrac{a^2+n^2-2mn}{a^2-n^2},\]于是原命题得证.
答案
解析
备注