设 $\triangle ABC$ 的内角 $A,B,C$ 所对应的边长分别为 $a,b,c$．已知 $a+b+c=16$，求 $b^2\cos^2\dfrac{C}{2}+c^2\cos^2\dfrac{B}{2}+2bc\cos\dfrac{B}{2}\cos\dfrac{C}{2}\sin\dfrac{A}{2}$ 的值．
【难度】
【出处】
2012年全国高中数学联赛江苏省复赛（一试）
【标注】
【答案】
$64$
【解析】
如图，延长 $BC$ 至 $E$，使 $CE=AC=b$，延长 $CB$ 至 $F$，使 $BF=AB=c$，连接 $AE,AF$．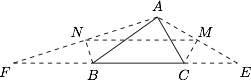
设 $AE,AF$ 的中点分别 $M,N$，则$$AM=b\cos\dfrac{C}{2},AN=c\cos\dfrac{B}{2},$$且$$\angle MAN=\angle A+\dfrac12(\angle B+\angle C)=\dfrac{\pi}{2}+\dfrac{A}{2},$$所以原式的值为$$AM^2+AN^2-2AM\cdot AN\cos\angle MAN=MN^2=64.$$
设 $AE,AF$ 的中点分别 $M,N$，则$$AM=b\cos\dfrac{C}{2},AN=c\cos\dfrac{B}{2},$$且$$\angle MAN=\angle A+\dfrac12(\angle B+\angle C)=\dfrac{\pi}{2}+\dfrac{A}{2},$$所以原式的值为$$AM^2+AN^2-2AM\cdot AN\cos\angle MAN=MN^2=64.$$
答案
解析
备注
