已知 $\triangle ABC$ 中 $A,B,C$ 的对边分别为 $a,b,c$,且 $a+b+c=10$,求 $b^2\cos^2\dfrac C2+c^2\cos^2\dfrac B2+2bc\cos\dfrac B2\cos\dfrac C2\sin\dfrac A2$ 的值.
【难度】
【出处】
无
【标注】
【答案】
$25$
【解析】
如图,过 $A$ 分别作 $B,C$ 的外角平分线的垂线,垂足分别为 $M,N$,与直线 $BC$ 分别交于 $P,Q$,所求代数式即$$MN^2=\dfrac 14PQ^2=25.$$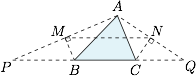

答案
解析
备注