如图所示，在 $\triangle ABC$ 中，$X,Y$ 是直线 $BC$ 上两点（$X,B,C,Y$ 顺次排列），使得$$BX\cdot AC=CY\cdot AB.$$设 $\triangle ACX,\triangle ABY$ 的外心分别为 $O_1,O_2$，直线 $O_1O_2$ 与 $AB,AC$ 分别交于点 $U,V$．证明：$\triangle AUV$ 是等腰三角形．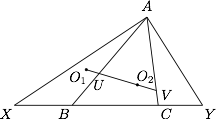
【难度】
【出处】
2016年全国高中数学联赛（二试）
【标注】
【答案】
略
【解析】
如图，设 $\triangle ABC$ 的外心为 $O$，连结 $OO_{1},OO_{2}$，过点 $O,O_{1},O_{2}$ 分别作直线 $BC$ 的垂线，垂足分别为 $D,D_{1},D_{2}$．作 $O_{1}K\perp OD$ 于点 $K$．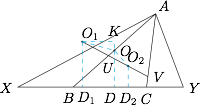
我们证明 $OO_{1}=OO_{2}$．在直角三角形 $OKO_{1}$ 中，\[OO_{1}=\dfrac{O_{1}K}{\sin\angle O_{1}OK}.\]由外心的性质，$OO_{1}\perp AC$，又 $OD\perp BC$，故 $\angle O_{1}OK=\angle ACB$．而 $D,D_{1}$ 分别是 $BC,CX$ 的中点，所以\[DD_{1}=CD_{1}-CD=\dfrac{1}{2}CX-\dfrac{1}{2}BC=\dfrac{1}{2}BX.\]因此\[OO_{1}=\dfrac{O_{1}K}{\sin \angle O_{1}OK}=\dfrac{DD_{1}}{\sin \angle ACB}=\dfrac{\dfrac{1}{2}BX}{\dfrac{AB}{2R}}=R\cdot \dfrac{BX}{AB},\]这里 $R$ 是 $\triangle ABC$ 的外接圆半径．同理 $OO_{2}=R\cdot \dfrac{CY}{AC}$．由已知条件可得 $\dfrac{BX}{AB}=\dfrac{CY}{AC}$，故 $OO_{1}=OO_{2}$．由于 $OO_{1}=OO_{2}$，故 $\angle OO_{1}O_{2}=\angle OO_{2}O_{1}$，从而 $\angle AUV=\angle AVU$．这样 $AU=AV$，即 $\triangle AUV$ 是等腰三角形．
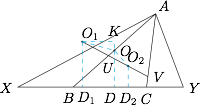我们证明 $OO_{1}=OO_{2}$．在直角三角形 $OKO_{1}$ 中，\[OO_{1}=\dfrac{O_{1}K}{\sin\angle O_{1}OK}.\]由外心的性质，$OO_{1}\perp AC$，又 $OD\perp BC$，故 $\angle O_{1}OK=\angle ACB$．而 $D,D_{1}$ 分别是 $BC,CX$ 的中点，所以\[DD_{1}=CD_{1}-CD=\dfrac{1}{2}CX-\dfrac{1}{2}BC=\dfrac{1}{2}BX.\]因此\[OO_{1}=\dfrac{O_{1}K}{\sin \angle O_{1}OK}=\dfrac{DD_{1}}{\sin \angle ACB}=\dfrac{\dfrac{1}{2}BX}{\dfrac{AB}{2R}}=R\cdot \dfrac{BX}{AB},\]这里 $R$ 是 $\triangle ABC$ 的外接圆半径．同理 $OO_{2}=R\cdot \dfrac{CY}{AC}$．由已知条件可得 $\dfrac{BX}{AB}=\dfrac{CY}{AC}$，故 $OO_{1}=OO_{2}$．由于 $OO_{1}=OO_{2}$，故 $\angle OO_{1}O_{2}=\angle OO_{2}O_{1}$，从而 $\angle AUV=\angle AVU$．这样 $AU=AV$，即 $\triangle AUV$ 是等腰三角形．
答案
解析
备注
