如图,$P$ 是抛物线 $y^2=2x$ 上的动点,点 $B$,$C$ 在 $y$ 轴上,圆 $(x-1)^2+y^2=1$ 内切于 $\triangle PBC$,求 $\triangle PBC$ 面积的最小值.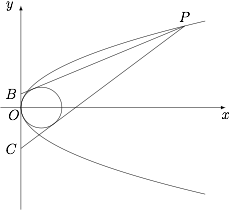

【难度】
【出处】
无
【标注】
【答案】
$8$
【解析】
设 $P(x_0,y_0)$,$B(0,b)$,$C(0,c)$,不妨设 $b>c$.
直线 $PB$ 的方程:$y-b=\dfrac {y_0-b}{x_0}x$,化简得$$(y_0-b)x-x_0y+x_0b=0.$$又圆心 $(1,0)$ 到 $PB$ 的距离为 $1$,即$$\dfrac {|y_0-b+x_0b|}{\sqrt {(y_0-b)^2+x_0^2}}=1,$$故$$(y_0-b)^2+x_0^2=(y_0-b)^2+2x_0b(y_0-b)+x_0^2b^2,$$易知 $x_0>2$,上式化简得$$(x_0-2)b^2+2y_0b-x_0=0,$$同理有$$(x_0-2)c^2+2y_0c-x_0=0,$$所以$$b+c=\dfrac {-2y_0}{x_0-2},\quad bc=\dfrac {- x_0}{x_0-2},$$则$$(b-c)^2=\dfrac {4x_0^2+4y_0^2-8x_0}{(x_0-2)^2}.$$因为 $P(x_0,y_0)$ 是抛物线上的点,故有 $y_0^2=2x_0$,则$$(b-c)^2=\dfrac {4x_0^2}{(x_0-2)^2},$$于是$$b-c=\dfrac {2x_0}{x_0-2},$$所以\[\begin{split}S_{\triangle PBC} &=\dfrac 12(b-c)\cdot x_0\\&=\dfrac {x_0}{x_0-2}\cdot x_0 \\&=(x_0-2)+\dfrac {4}{x_0-2}+4\\&\geqslant 2\sqrt 4+4=8,\end{split}\]当 $(x_0-2)^2=4 $ 时,上式取等号,此时 $x_0=4$,$y_0=\pm 2\sqrt 2$.
因此 $S_{\triangle PBC}$ 的最小值为 $8$.
直线 $PB$ 的方程:$y-b=\dfrac {y_0-b}{x_0}x$,化简得$$(y_0-b)x-x_0y+x_0b=0.$$又圆心 $(1,0)$ 到 $PB$ 的距离为 $1$,即$$\dfrac {|y_0-b+x_0b|}{\sqrt {(y_0-b)^2+x_0^2}}=1,$$故$$(y_0-b)^2+x_0^2=(y_0-b)^2+2x_0b(y_0-b)+x_0^2b^2,$$易知 $x_0>2$,上式化简得$$(x_0-2)b^2+2y_0b-x_0=0,$$同理有$$(x_0-2)c^2+2y_0c-x_0=0,$$所以$$b+c=\dfrac {-2y_0}{x_0-2},\quad bc=\dfrac {- x_0}{x_0-2},$$则$$(b-c)^2=\dfrac {4x_0^2+4y_0^2-8x_0}{(x_0-2)^2}.$$因为 $P(x_0,y_0)$ 是抛物线上的点,故有 $y_0^2=2x_0$,则$$(b-c)^2=\dfrac {4x_0^2}{(x_0-2)^2},$$于是$$b-c=\dfrac {2x_0}{x_0-2},$$所以\[\begin{split}S_{\triangle PBC} &=\dfrac 12(b-c)\cdot x_0\\&=\dfrac {x_0}{x_0-2}\cdot x_0 \\&=(x_0-2)+\dfrac {4}{x_0-2}+4\\&\geqslant 2\sqrt 4+4=8,\end{split}\]当 $(x_0-2)^2=4 $ 时,上式取等号,此时 $x_0=4$,$y_0=\pm 2\sqrt 2$.
因此 $S_{\triangle PBC}$ 的最小值为 $8$.
答案
解析
备注