如图，点 $A$ 坐标为 $(2,0)$，以 $OA$ 为边在第一象限内作等边 $\triangle OAB$，点 $C$ 为 $x$ 轴上一动点，且在点 $A$ 右侧，连接 $BC$，以 $BC$ 为边在第一象限内作等边 $\triangle BCD$，连接 $AD$ 交 $BC$ 于点 $E$．
【难度】
【出处】
无
【标注】
-
当点 $C$ 运动到使 $AC^2=AE\cdot AD$ 时，经过 $O,B,C$ 三点的抛物线为 $y_1$．试问：$y_1$ 上是否存在动点 $P$，使 $\triangle BEP$ 为直角三角形且 $BE$ 为直角边？若存在，求出点 $P$ 坐标；若不存在，说明理由；标注答案存在，点 $P$ 的坐标为 $(0,0)$，$(-2,-4\sqrt 3)$ 或 $(3,\sqrt 3)$解析由 $AC^2=AE\cdot AD$，可得 $\dfrac{AC}{AE}=\dfrac{AD}{AC}$．
而 $\angle EAC=\angle CAD$，
所以 $\triangle AEC\backsim \triangle ACD$，
所以 $\angle ECA=\angle CDA$．
由“共顶点模型”可得 $\triangle OBC\cong \triangle ABD$，
所以 $\angle BDA=\angle BCO=\angle CDA$，
从而得到 $AD\perp BC$，$BE=CE$．
所以 $AC=AB=AO=2$，
所以 $\angle ABC=\angle ACB=30^\circ$，
从而 $\angle ABE=ACD=90^\circ$．
所以 $CD=\sqrt 3AC=2\sqrt 3$，即点 $D(4,2\sqrt 3)$．
由 $A,D$ 点的坐标可得直线 $AD$ 解析式为 $y=\sqrt 3x-2\sqrt 3$．
易得点 $B$ 坐标为 $(1,\sqrt 3)$，
则抛物线 $y_1$ 解析式为 $y=-\dfrac{\sqrt 3}3x(x-4)$．
联立方程组 $\begin{cases}y=-\dfrac{\sqrt 3}3x(x-4),\\y=\sqrt 3x-2\sqrt 3.\end{cases}$
解得 $\begin{cases}x_1=-2,\\y_1=-4\sqrt 3,\end{cases}$ $\begin{cases}x_2=3,\\y_2=\sqrt 3.\end{cases}$
所以满足条件的点 $P$ 的坐标为 $(0,0)$，$(-2,-4\sqrt 3)$ 或 $(3,\sqrt 3)$． -
在第1问的条件下，将 $y_1$ 沿 $x$ 轴翻折得 $y_2$，设 $y_1$ 与 $y_2$ 组成的图形为 $M$，函数 $y=\sqrt 3x+\sqrt 3m$ 的图象 $l$ 与 $M$ 有公共点．试求当 $l$ 与 $M$ 的公共点为 $3$ 个时 $m$ 的取值．标注答案$m$ 的值为 $\dfrac 1{12}$ 或 $-\dfrac {49}{12}$解析由题意可得抛物线 $y_2$ 解析式为 $y=\dfrac{\sqrt 3}3x(x-4)$．
如图，当直线 $l_1$ 与抛物线 $y_1$ 只有一个公共点时，直线 $l_1$ 与图象 $M$ 公共点恰好为 $3$ 个．
同理，当直线 $l_2$ 与抛物线 $y_2$ 只有一个公共点时，直线 $l_2$ 与图象 $M$ 公共点也恰好为 $3$ 个．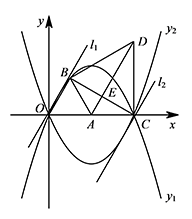
① 联立方程组 $\begin{cases}y=-\dfrac{\sqrt 3}3x(x-4),\\y=\sqrt 3x+\sqrt 3m,\end{cases}$
若方程组的解唯一，则可得 $m=\dfrac 1{12}$；
② 联立方程组 $\begin{cases}y=\dfrac{\sqrt 3}3x(x-4),\\y=\sqrt 3x+\sqrt 3m,\end{cases}$
若方程组的解唯一，则可得 $m=-\dfrac {49}{12}$．
综上可得，满足题意的 $m$ 的值为 $\dfrac 1{12}$ 或 $-\dfrac {49}{12}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
