在 $\triangle ABC$ 中，$D,E$ 是边 $BC$ 上的点，且 $BD=CE$，求证：$AB+AC>AD+AE$．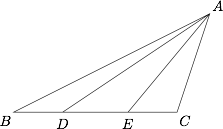
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图，分别以 $B,C$ 和 $D,E$ 为焦点作过点 $A$ 的椭圆，则设椭圆方程分别为\[\dfrac{x^{2}}{a_{1}^{2}}+\dfrac{y^{2}}{b_{1}^{2}}=1,\dfrac{x^{2}}{a_{2}^{2}}+\dfrac{y^{2}}{b_{2}^{2}}=1,\]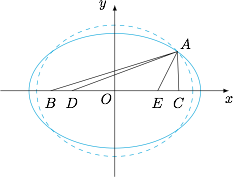
且\[a_{1}^{2}-b_{1}^{2}=\left(\dfrac{BC}{2}\right)^{2}>\left(\dfrac{DE}{2}\right)^{2}=a_{2}^{2}-b_{2}^{2}.\]由于两椭圆交于 $A(x_{0},y_{0})$，所以\[\dfrac{x_{0}^{2}}{a_{1}^{2}}+\dfrac{y_{0}^{2}}{b_{1}^{2}}=\dfrac{x_{0}^{2}}{a_{2}^{2}}+\dfrac{y_{0}^{2}}{b_{2}^{2}},\]若 $a_{1}^{2}\leqslant a_{2}^{2}$，则 $b_{1}^{2}\leqslant b_{2}^{2}$，矛盾．因此 $a_{1}^{2}>a_{2}^{2}$，即 $2a_{1}>2a_{2}$，也即\[AB+AC>AD+AE.\]
且\[a_{1}^{2}-b_{1}^{2}=\left(\dfrac{BC}{2}\right)^{2}>\left(\dfrac{DE}{2}\right)^{2}=a_{2}^{2}-b_{2}^{2}.\]由于两椭圆交于 $A(x_{0},y_{0})$，所以\[\dfrac{x_{0}^{2}}{a_{1}^{2}}+\dfrac{y_{0}^{2}}{b_{1}^{2}}=\dfrac{x_{0}^{2}}{a_{2}^{2}}+\dfrac{y_{0}^{2}}{b_{2}^{2}},\]若 $a_{1}^{2}\leqslant a_{2}^{2}$，则 $b_{1}^{2}\leqslant b_{2}^{2}$，矛盾．因此 $a_{1}^{2}>a_{2}^{2}$，即 $2a_{1}>2a_{2}$，也即\[AB+AC>AD+AE.\]
答案
解析
备注
