在 $\triangle ABC$ 中,$D,E$ 是边 $BC$ 上的点,且 $BD=CE$,求证:$AB+AC>AD+AE$.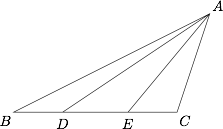

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图,作 $AA'\parallel BD$,且 $AA'=BD$,则题中不等式即\[AB+A'E>AE+A'B,\]显然成立.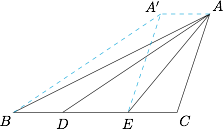

答案
解析
备注