查看数据源：59fad8786ee16400083d2855
直线 $l:kx-y-2=0$ 与直线 $x+2y-2=0$ 的交点在第一象限，则直线 $l$ 的倾斜角 $\theta$ 的取值范围是 \((\qquad)\)
A: $\left(\dfrac{\pi}{4},\dfrac{\pi}{2}\right)$
B: $\left(\dfrac{\pi}{2},\pi\right)$
C: $\left(0,\dfrac{\pi}{4}\right)$
D: $\left(0,\dfrac{\pi}{2}\right)$
【难度】
【出处】
2010年第二十一届“希望杯”全国数学邀请赛高一（一试）
【标注】
  • 知识点
    >
    解析几何
    >
    直线
    >
    直线的方程
【答案】
A
【解析】
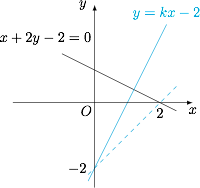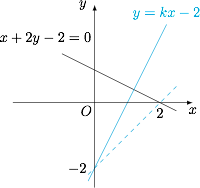如图．由图可知，若两直线交点在第一象限，则 $k>1$，所以直线 $l$ 的倾斜角 $\theta$ 的取值范围是 $\left(\dfrac{\pi}{4},\dfrac{\pi}{2}\right)$．
题目 答案 解析 备注
0.110585s