题目 已知关于 $x$ 的一元二次方程 ${x^2}+2x+\dfrac{k-1}{2} = 0$ 有两个不相等的实数根，$k$ 为正整数．<br><img src="/static/images/846235b990ffa472cde83fc2a123e43c.png" class="img-responsive" /> 问题1 当此方程有一根为零时，直线 $y=x+2$ 与关于 $x$ 的二次函数 $y={x^2} + 2x + \dfrac{k - 1}{2}$ 的图象交于 $A,B$ 两点，若 $M$ 是线段 $AB$ 上的一个动点，过点 $ M $ 作 $MN\perp x$ 轴，交二次函数的图象于点 $N$，求线段 $MN$ 的最大值及此时点 $M$ 的坐标； 答案1 当 $m=-\dfrac 12$ 时，$MN$ 的长度最大值为 $\dfrac 94$，此时点 $M$ 的坐标为 $\left(-\dfrac 12,\dfrac 32\right)$ 解析1 因为关于 $x$ 的一元二次方程 $x^2+2x+\dfrac {k-1}{2}=0$ 有两个不相等的实数根，<br/>所以 $ \Delta =b^2-4ac=4-4\times \dfrac {k-1}{2}>0$，<br/>所以 $ k-1<2$，<br/>所以 $ k<3$．<br/>因为 $ k$ 为正整数，<br/>所以 $ k$ 的值是 $1$，$2$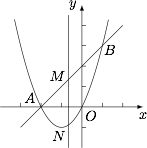．<img src="/static/images/491f581c433783ed5161bb735b75e884.png" class="img-responsive" />把 $x=0$ 代入方程 $x^2+2x+\dfrac {k-1}{2}=0$ 得 $k=1,$ 此时二次函数为 $y=x^2+2x$，<br/>此时直线 $y=x+2$ 与二次函数 $y=x^2+2x$ 的交点为 $A\left(-2,0\right)$，$B\left(1,3\right)$，<br/>由题意可设 $M\left(m,m+2\right)$，其中 $-2<m<1$，则 $N\left(m,m^2+2m\right)$，<br/>$\begin{split}MN&=m+2-\left(m^2+2m\right) \\&=-m^2-m+2\\&=-\left(m+\dfrac 12\right)^2+\dfrac 94,\end{split}$<br/>所以当 $m=-\dfrac 12$ 时，$MN$ 的长度最大值为 $\dfrac 94$，此时点 $M$ 的坐标为 $\left(-\dfrac 12,\dfrac 32\right)$． 备注1 问题2 将 $(1)$ 中的二次函数图象 $ x $ 轴下方的部分沿 $x$ 轴翻折到 $x$ 轴上方，图象的其余部分保持不变，翻折后的图象与原图象 $x$ 轴上方的部分组成一个“$ W $”形状的新图象，若直线 $y=\dfrac{1}{2}x+b$ 与该新图象恰好有三个公共点，求 $b$ 的值． 答案2 $b=1$ 或 $b=\dfrac {25}{16}$ 解析2 当 $y=\dfrac 12x+b$ 过点 $A$ 时，直线与新图象有 $3$ 个公共点（如图所示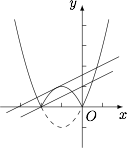）．<img src="/static/images/f3cb4c7fc5333cef8ae702dbb7e8af55.png" class="img-responsive" />把 $A\left(-2,0\right)$ 代入 $y=\dfrac 12x+b$ 得 $b=1$；<br/>当 $y=\dfrac 12x+b$ 与新图象的封闭部分有一个公共点时，直线与新图象有 $3$ 个公共点，<br/>由于新图象的封闭部分与原图象的封闭部分关于 $x$ 轴对称，<br/>所以其解析式为 $y=-x^2-2x$，<br/>所以 $ \begin{cases} y=\dfrac 12x+b, \\ y=-x^2-2x\end{cases}$ 有一组解，此时 $-x^2-\dfrac 52x-b=0$ 有两个相等的实数根，<br/>则 $\left(\dfrac 52\right)^2-4b=0$，<br/>所以 $b=\dfrac {25}{16}$，<br/>综上所述，$b=1$ 或 $b=\dfrac {25}{16}$． 备注2