如图，在平面直角坐标系 $xOy$ 中，矩形 $OABC$ 的边 $OA$ 在 $y$ 轴的正半轴上，$OC$ 在 $x$ 轴的正半轴上，$OA=1$，$OC=2$，点 $D$ 在边 $OC$ 上且 $OD=\dfrac 54$．
【难度】
【出处】
无
【标注】
-
求直线 $AC$ 的解析式；标注答案直线 $AC$ 的解析式为 $y=-\dfrac 12x+1$解析由已知可得点 $A\left(0,1\right)$，点 $C\left(2,0\right)$，
从而直线 $AC$ 的解析式为 $y=-\dfrac 12x+1$． -
在 $y$ 轴上是否存在点 $P$，直线 $PD$ 与矩形对角线 $AC$ 交于点 $M$，使得 $\triangle DMC$ 为等腰三角形？若存在，直接写出所有符合条件的点 $P$ 的坐标；若不存在，请说明理由．标注答案存在符合条件的点 $P$，坐标为 $\left(0,-\dfrac {5\left(\sqrt 5+2\right)}4\right)$，$\left(0,\dfrac 53\right)$ 或 $\left(0,-\dfrac 58\right)$解析
解法一 设 $M\left(m,-\dfrac 12m+1\right)$，则 $0\leqslant m<2$，
由平面内两点之间的距离公式可得 $CD^2=\dfrac 9{16}$，
$CM^2=\left(2-m\right)^2+\left(-\dfrac 12m+1\right)^2$，
$DM^2=\left(m-{\dfrac 54}\right)^2+\left({-\dfrac 12}m+1\right)^2$．
① 当 $CD=CM$ 时，有 $\dfrac 9{16}=\left(-\dfrac 12m+1\right)^2+\left(2-m\right)^2$，
解得 $m_1=2-{\dfrac {3\sqrt 5}{10}}$，$m_2=2+{\dfrac {3\sqrt 5}{10}}$（舍），
所以点 $M$ 的坐标为 $\left(2-{\dfrac {3\sqrt 5}{10}},\dfrac {3\sqrt 5}{20}\right)$．
从而直线 $DM$ 的解析式为 $y=\left(\sqrt 5+2\right)x-\dfrac {5\left(\sqrt 5+2\right)}4$，
可得点 $P$ 的坐标为 $\left(0,-\dfrac {5\left(\sqrt 5+2\right)}4\right)$；
② 当 $DM=DC$ 时，有 $\dfrac 9{16}=\left(m-{\dfrac 54}\right)^2+\left({-\dfrac 12}m+1\right)^2$，
解得 $m_3=2$（舍），$m_4=\dfrac 45$，
所以 $M$ 的坐标为 $\left(\dfrac 45,\dfrac 35\right)$．
从而直线 $DM$ 的解析式为 $y=-\dfrac 43x+\dfrac 53$，
可得点 $P$ 的坐标为 $\left(0,\dfrac 53\right)$；
③ 当 $MD=MC$ 时，有 $\left(m-{\dfrac 54}\right)^2+\left({-\dfrac 12}m+1\right)^2=\left(-\dfrac 12m+1\right)^2+\left(2-m\right)^2$，
解得 $m_5=\dfrac {13}8$，
所以点 $M$ 的坐标为 $\left(\dfrac {13}8,\dfrac 3{16}\right)$．
从而直线 $DM$ 的解析式为 $y=\dfrac 12x-\dfrac 58$，
可得点 $P$ 的坐标为 $\left(0,-\dfrac 58\right)$．
综上所得，符合条件的点 $P$ 的坐标为 $\left(0,-\dfrac {5\left(\sqrt 5+2\right)}4\right),\left(0,\dfrac 53\right),\left(0,-\dfrac 58\right)$．解法二 ① 如图，当 $MD=MC$ 时，有 $x_M=\dfrac 12(x_c+x_D)=\dfrac {13}8$，
将其代入直线 $AC$ 解析式得 $y_M=\dfrac 3{16}$．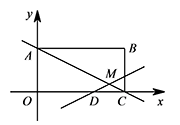
所以直线 $DM$ 的解析式为 $y=\dfrac 12x-\dfrac 58$，
可得点 $P$ 的坐标为 $\left(0,-\dfrac 58\right)$；
② 如图，当 $CD=CM$ 时，设直线 $DM$ 与 $AB$ 交于点 $N$．
因为 $\angle CDM=\angle CMD=\angle AMN=\angle ANM$，
所以 $AM=AN=\sqrt 5-\dfrac 34$，
所以点 $N$ 的坐标为 $\left({\sqrt 5-\dfrac 34},1\right)$，
从而直线 $DN$ 解析式为 $y=\left(\sqrt 5+2\right)x-\dfrac {5\left(\sqrt 5+2\right)}4$，
可得点 $P$ 的坐标为 $\left(0,-\dfrac {5\left(\sqrt 5+2\right)}4\right)$；
③ 如图，当 $DM=DC$ 时，作 $DH\perp AC$ 于点 $H$，作 $HE\perp OC$ 于点 $E$．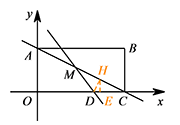
易得 $\triangle CDH\sim \triangle CAO\sim \triangle CHE$，
所以 $CH=\dfrac {3\sqrt 5}{10}$，$EH=\dfrac 3{10}$，$CE=\dfrac 35$．
从而点 $H$ 的坐标为 $\left(\dfrac 75,\dfrac 3{10}\right)$，
所以点 $M$ 的坐标为 $\left(\dfrac 45,\dfrac 35\right)$，
所以直线 $DM$ 的解析式为 $y=-\dfrac 43x+\dfrac 53$，
可得点 $P$ 的坐标为 $\left(0,\dfrac 53\right)$．
综上所得，符合条件的点 $P$ 的坐标为 $\left(0,-\dfrac {5\left(\sqrt 5+2\right)}4\right),\left(0,\dfrac 53\right),\left(0,-\dfrac 58\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
