正方体 $ABCD-A_1B_1C_1D_1$ 中,过顶点 $A_1$ 作直线 $AC$ 和直线 $BC_1$ 所成的角均为 $60^\circ$,则这样的直线 $l$ 的条数为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
设异面直线 $a,b$ 成 $\alpha$ 角,且 $\alpha\in\left(0,\dfrac{\pi}{2}\right]$,$A$ 为空间一点,且过 $A$ 与 $a,b$ 都成 $\theta$ 角的直线条数:$$\begin{array}{|c|c|c|c|c|c|c|}\hline \theta &0\leqslant\theta<\dfrac{\alpha}{2} &\theta=\dfrac{\alpha}{2} &\dfrac{\alpha}{2}<\theta<\dfrac{\pi-\alpha}{2} &\theta=\dfrac{\pi-\alpha}{2} &\dfrac{\pi-\alpha}{2}<\theta<\dfrac{\pi}{2} & \theta=\dfrac{\pi}{2}\\ \hline \text{条数}&0 &1&2 &3 &4 &1\\ \hline\end{array}$$如图,$BC_1$ 与 $AC$ 成 $60^\circ$,所以满足条件的直线 $l$ 有 $3$ 条.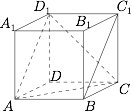

题目
答案
解析
备注