查看数据源：5927e60d50ce840009d770b0
如图，已知二次函数 $L_1:y=ax^2-2ax+a+3\left(a>0\right)$ 和二次函数 $L_2:y=-a\left(x+1\right)^2+1\left(a>0\right)$ 图象的顶点分别为 $M,N$，与 $y$ 轴分别交于点 $E,F$．若二次函数 $L_2$ 的图象与 $x$ 轴的右交点为 $A\left(m,0\right)$，当 $\triangle AMN$ 为等腰三角形时，求方程 $-a\left(x+1\right)^2+1=0$ 的解．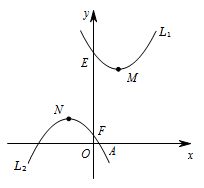
【难度】
【出处】
无
【标注】
  • 题型
    >
    代几综合
    >
    等腰三角形的存在性
【答案】
当 $\triangle AMN$ 为等腰三角形时，方程 $-a\left(x+1\right)^2+1=0$ 的解为 $x_1=\sqrt 7-1$，$x_2=-1-\sqrt 7$ 或者 $x_1=2$，$x_2=-4$
【解析】
由二次函数 $L_1:y=ax^2-2ax+a+3=a(x-1)^2+3$，
得点 $M$ 的坐标为 $(1,3)$．
由二次函数 $L_2:y=-a\left(x+1\right)^2+1$，
得点 $N$ 的坐标为 $(-1,1)$．
所以 $\triangle AMN$ 中，$MN^2=8$，$AM^2=(m-1)^2+9$，$AN^2=(m+1)^2+1$．
$\triangle AMN$ 为等腰三角形可分如下三种情况：
① 当 $MN=AN$ 时，有 $(m+1)^2+1=8$，
解得 $m_1=\sqrt 7-1$，$m_2=-\sqrt 7-1$（不合题意，舍去）．
所以点 $A\left(\sqrt 7-1,0\right)$，
由抛物线的对称性可得 $L_2$ 与 $x$ 轴的左交点坐标为 $\left(-\sqrt 7-1,0\right)$，
所以方程 $-a\left(x+1\right)^2+1=0$ 的解为 $x_1=\sqrt 7-1$，$x_2=-\sqrt 7-1$．
② 当 $AM=AN$ 时，有 $(m-1)^2+9=(m+1)^2+1$，
解得 $m=2$．
所以点 $A\left(2,0\right)$，
由抛物线的对称性可得 $L_2$ 与 $x$ 轴的左交点坐标为 $\left(-4,0\right)$，
所以方程 $-a\left(x+1\right)^2+1=0$ 的解为 $x_1=2$，$x_2=-4$．
③ 当 $MN=AM$ 时，$(m-1)^2+9=8$，
方程无实数解，故此情况不存在．
综上所述，当 $\triangle AMN$ 为等腰三角形时，方程 $-a\left(x+1\right)^2+1=0$ 的解为 $x_1=\sqrt 7-1$，$x_2=-1-\sqrt 7$ 或者 $x_1=2$，$x_2=-4$．
答案 解析 备注
0.110157s