下列网格中的六边形 $ABCDEF$ 是由边长为 $6$ 的正方形左上角剪去边长为 $2$ 的正方形所得,该六边形按一定的方法可剪拼成一个正方形.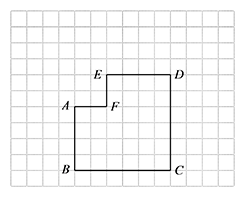
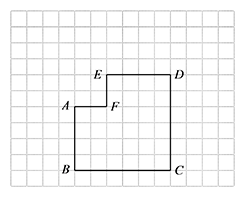
【难度】
【出处】
无
【标注】
-
根据剪拼前后图形的面积关系求出拼成的正方形的边长;标注答案$4\sqrt 2$解析略
-
如图甲,把六边形 $ABCDEF$ 沿 $EH,BG$ 剪成 ①、②、③ 三个部分,请在图甲中画出将 ②、③ 与 ① 拼成的正方形,然后标出 ②、③ 变动后的位置;
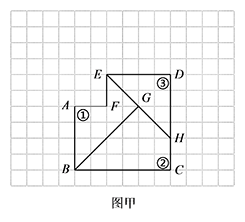 标注答案如图:
标注答案如图: 解析略
解析略 -
在图乙中画出一种与图甲不同位置的两条剪裁线,并画出将此六边形剪拼成的正方形.
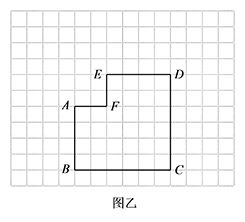 标注答案如图:
标注答案如图: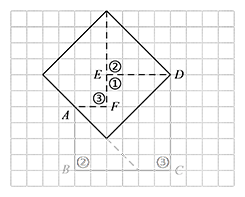
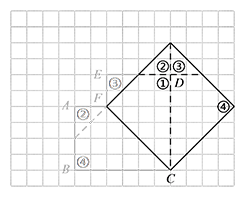 解析略
解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3