如图,在平面直角坐标系中,已知抛物线 $y=ax^2+bx$ 的对称轴为 $x=\dfrac34$,且经过点 $A\left(2,1\right)$.点 $P$ 是抛物线上的动点,$P$ 的横坐标为 $m$($0<m<2$).过点 $P$ 作 $PB\perp x$ 轴,垂足为点 $B$,$PB$ 交 $OA$ 于点 $C$.点 $O$ 关于直线 $PB$ 的对称点为 $D$,连接 $CD,AD$.过点 $A$ 作 $AE\perp x$ 轴,垂足为点 $E$.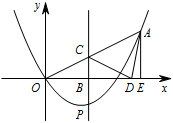

【难度】
【出处】
无
【标注】
-
当 $m=$
所以 $CD=CO$,且点 $D\left(2m,0\right)$.
从而 $C_{\triangle ACD}=AC+CD+AD=AO+AD$,
因为 $AO$ 为定值,所以 $AD$ 最短时,$\triangle ACD$ 周长最小.
而当 $D$ 与 $E$ 重合时,$AD$ 最小,
此时 $D$ 点的坐标为 $\left(2,0\right)$,
所以 $m=1$. -
若 $\triangle ACD$ 为等腰三角形,求出所有符合条件的点 $P$ 的坐标.标注答案符合条件的点 $P$ 的坐标分别为 $\left(1,-\dfrac12\right)$,$\left(\dfrac{12}{11},-\dfrac{54}{121}\right)$,$\left(\dfrac{10}{11},-\dfrac{65}{121}\right)$解析依题可得 $\begin{cases}
-\dfrac{b}{2a}=\dfrac34,\\4a+2b=1,
\end{cases}$
解得 $\begin{cases}
a=1,\\b=-\dfrac32.
\end{cases}$
所以抛物线的解析式为 $y=x^2-\dfrac32x$.
依题意得 $B\left(m,0\right)$,$P\left(m,m^2-\dfrac 32m\right)$.
在 $\mathrm {Rt}\triangle OBC$ 中,$OC=\sqrt{OB^2+BC^2}=\sqrt{m^2+\left(\dfrac12m\right)^2}=\dfrac{\sqrt 5}2m$,
从而 $CD=OC=\dfrac{\sqrt5}2{m}$.
在 $\mathrm {Rt}\triangle AOE$ 中,$OA=\sqrt{OE^2+AE^2}=\sqrt{2^2+1^2}=\sqrt5$,
所以 $AC=OA-OC=\sqrt5-\dfrac{\sqrt5}{2}m$.
在 $\mathrm {Rt}\triangle ADE$ 中,$AD=\sqrt{AE^2+DE^2}=\sqrt{1^2+\left(2-2m\right)^2}=\sqrt{4m^2-8m+5}$.
若 $\triangle ACD$ 为等腰三角形,可分三种情况讨论:
① 若 $AC=CD$,即 $\sqrt5-\dfrac{\sqrt5}{2}m=\dfrac{\sqrt5}{2}m$,
解得 $m=1$,则此时 $P_1\left(1,-\dfrac12\right)$;
② 若 $AC=AD$,则有 $AC^2=AD^2$,即 $5-5m+\dfrac54m^2=4m^2-8m+5$,
解得 $m_1=0$,$m_2=\dfrac{12}{11}$.
而 $0<m<2$,所以 $m=\dfrac{12}{11}$,
所以此时 $P_2\left(\dfrac{12}{11},-\dfrac{54}{121}\right)$;
③ 若 $DA=DC$,则有 $DA^2=DC^2$,即 $4m^2-8m+5=\dfrac54m^2$,
解得 $m_1=\dfrac{10}{11}$,$m_2=2$,
而 $0<m<2$,所以 $m=\dfrac{10}{11}$,
所以此时 $P_3\left(\dfrac{10}{11},-\dfrac{65}{121}\right)$.
综上可得,当 $\triangle ACD$ 为等腰三角形时,点 $P$ 的坐标分别为 $\left(1,-\dfrac12\right)$,$\left(\dfrac{12}{11},-\dfrac{54}{121}\right)$,$\left(\dfrac{10}{11},-\dfrac{65}{121}\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2