如图,抛物线 $y=x^2-2x-3$ 的顶点为 $E$,该抛物线与 $x$ 轴交于 $A$、$B$ 两点,与 $y$ 轴交于点 $C$,且 $BO=OC=3AO$,直线 $y=-\dfrac 1 3x+1$ 与 $y$ 轴交于点 $D$ 在抛物线的对称轴上是否存在点 $P$,使 $\triangle PBC$ 是等腰三角形?若存在,请直接写出符合条件的 $ P $ 点坐标,若不存在,请说明理由.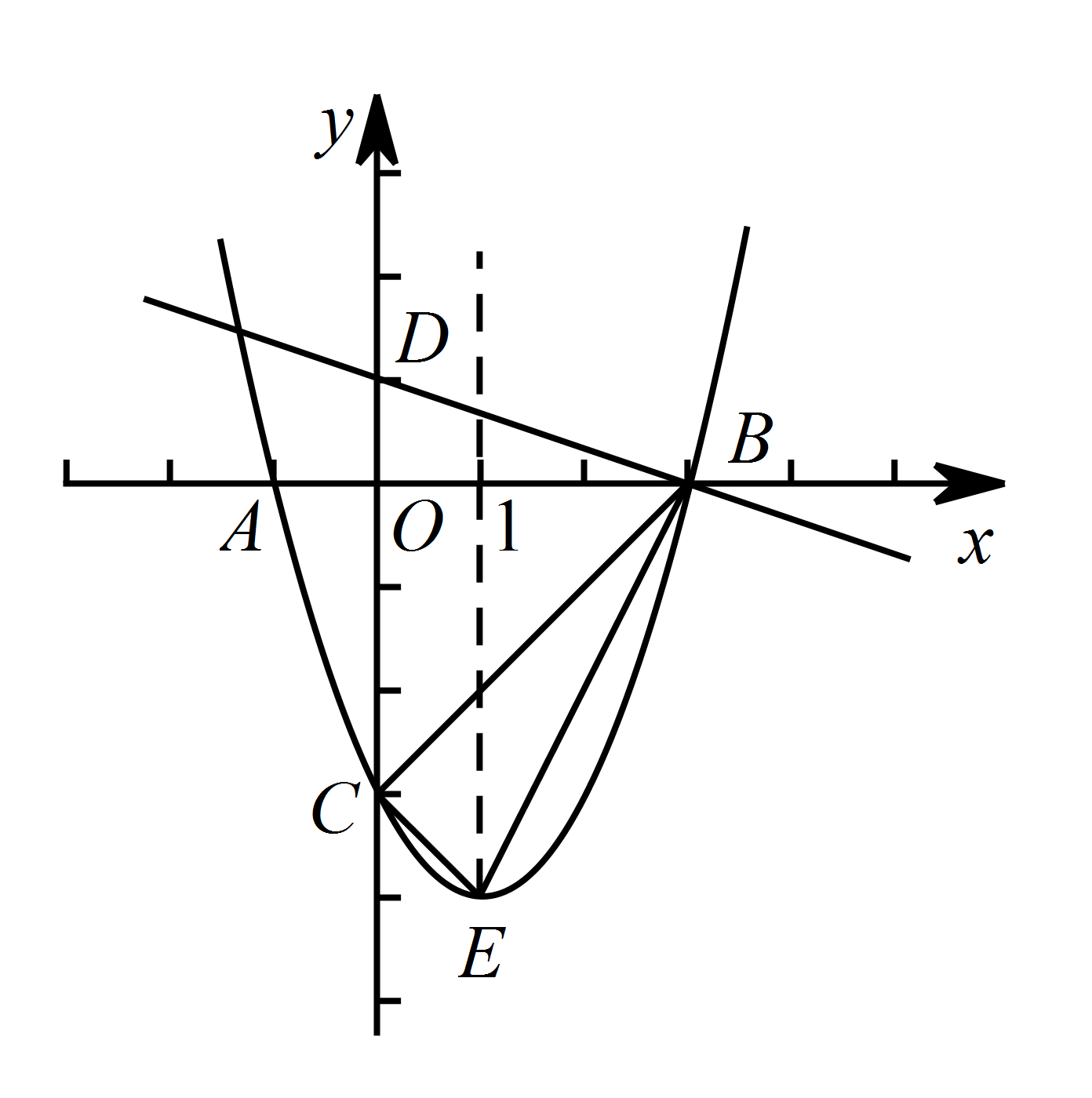

【难度】
【出处】
无
【标注】
【答案】
存在.符合条件的 $P$ 点坐标为 $\left(1,-1\right)$ 或 $\left(1,\sqrt {14}\right)$ 或 $\left(1,-\sqrt{14}\right)$ 或 $\left(1,-3+\sqrt {17}\right)$ 或 $\left(1,-3-\sqrt {17}\right)$
【解析】
设点 $P$ 的坐标为 $\left(1,m\right)$.
而点 $B\left(3,0\right)$,点 $C\left(0,-3\right)$,
所以 $BC=3\sqrt 2$,$PB=\sqrt {m^2+4}$,$PC=\sqrt {\left(m+3\right)^2+1}$.
$\triangle PBC$ 是等腰三角形有以下三种可能:
① 当 $PB=PC$ 时,即 $\sqrt{m^2+4}=\sqrt{\left(m+3\right)^2+1}$,
解得 $m=-1$,所以点 $P$ 坐标为 $\left(1,-1\right)$;
② 当 $PB=BC$ 时,即 $3\sqrt 2=\sqrt {m^2+4}$,
解得 $m=\pm \sqrt{14}$,所以点 $P$ 坐标为 $\left(1,\sqrt {14}\right)$ 或 $\left(1,-\sqrt{14}\right)$;
③ 当 $PC=BC$ 时,即 $3\sqrt 2=\sqrt {\left(m+3\right)^2+1}$,
解得 $m=-3\pm \sqrt{17}$,所以点 $P$ 坐标为 $\left(1,-3+\sqrt {17}\right)$ 或 $\left(1,-3-\sqrt{17}\right)$.
综上可得,符合条件的点 $P$ 坐标为 $\left(1,-1\right)$ 或 $\left(1,\sqrt {14}\right)$ 或 $\left(1,-\sqrt{14}\right)$ 或 $\left(1,-3+\sqrt {17}\right)$ 或 $\left(1,-3-\sqrt {17}\right)$.
而点 $B\left(3,0\right)$,点 $C\left(0,-3\right)$,
所以 $BC=3\sqrt 2$,$PB=\sqrt {m^2+4}$,$PC=\sqrt {\left(m+3\right)^2+1}$.
$\triangle PBC$ 是等腰三角形有以下三种可能:
① 当 $PB=PC$ 时,即 $\sqrt{m^2+4}=\sqrt{\left(m+3\right)^2+1}$,
解得 $m=-1$,所以点 $P$ 坐标为 $\left(1,-1\right)$;
② 当 $PB=BC$ 时,即 $3\sqrt 2=\sqrt {m^2+4}$,
解得 $m=\pm \sqrt{14}$,所以点 $P$ 坐标为 $\left(1,\sqrt {14}\right)$ 或 $\left(1,-\sqrt{14}\right)$;
③ 当 $PC=BC$ 时,即 $3\sqrt 2=\sqrt {\left(m+3\right)^2+1}$,
解得 $m=-3\pm \sqrt{17}$,所以点 $P$ 坐标为 $\left(1,-3+\sqrt {17}\right)$ 或 $\left(1,-3-\sqrt{17}\right)$.
综上可得,符合条件的点 $P$ 坐标为 $\left(1,-1\right)$ 或 $\left(1,\sqrt {14}\right)$ 或 $\left(1,-\sqrt{14}\right)$ 或 $\left(1,-3+\sqrt {17}\right)$ 或 $\left(1,-3-\sqrt {17}\right)$.
答案
解析
备注