如图，抛物线 $ y=x^2+2x-3$ 与 $x$ 轴交于 $A,B$ 两点，且 $B\left(1,0\right)$．已知直线 $y=\dfrac 2 3 x-\dfrac 4 9$ 分别与 $x$ 轴、$y$ 轴交于 $C,F$ 两点，点 $Q$ 是直线 $CF$ 下方的抛物线上的一个动点，过点 $Q$ 作 $y$ 轴的平行线，交直线 $CF$ 于点 $D$，点 $E$ 在线段 $CD$ 的延长线上，连接 $QE$，问：以 $QD$ 为腰的等腰 $\triangle QDE$ 的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．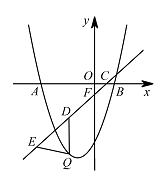
【难度】
【出处】
无
【标注】
【答案】
存在，以 $QD$ 为腰的等腰 $\triangle QDE$ 的面积最大值为 $\dfrac{54}{13}$
【解析】
如图，作 $QH\perp CF$ 于点 $H$．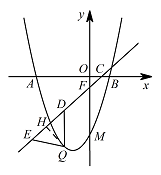
由直线 $y=\dfrac 2 3x-\dfrac 4 9$ 解析式可得点 $C\left(\dfrac 2 3,0\right),F\left(0,-\dfrac4 9\right)$，
所以 $\tan\angle OFC=\dfrac{OC}{OF}=\dfrac 3 2$．
因为 $DQ\parallel y$ 轴，
所以 $\angle QDH=\angle MFD=\angle OFC$，
所以 $\tan\angle HDQ=\dfrac 3 2$．
不妨记 $DQ=t$，则 $DH=\dfrac2 {\sqrt{13}} t$，$HQ=\dfrac3 {\sqrt{13}} t$．
因为 $\triangle QDE$ 是以 $DQ$ 为等腰的等腰三角形，
① 若 $DQ=DE$ 则 $S_{\triangle DEQ}=\dfrac1 2DE\cdot HQ=\dfrac{3\sqrt{13}}{26} t^2$；
② 若 $DQ=QE$，则 $S_{\triangle DEQ}=\dfrac1 2DE\cdot HQ=\dfrac1 2\times\dfrac4{\sqrt{13}}t\times\dfrac3{\sqrt{13}}t=\dfrac6{13} t^2$．
因为 $\dfrac{3\sqrt{13}}{26} t^2<\dfrac6{13} t^2$
所以当 $DQ=QE$ 时 $\triangle DEQ$ 的面积比 $DQ=DE$ 时大．
设点 $Q\left(x,x^2+2x-3\right)$，则点 $D\left(x,\dfrac2 3 x-\dfrac4 9\right)$．
所以 $DQ=t=\dfrac2 3x-\dfrac 4 9-\left(x^2+2x-3\right)=-x^2-\dfrac4 3 x+\dfrac{23}9$．
所以当 $x=-\dfrac 2 3$ 时，$t_{\max} =3.$
此时 $S_{\triangle DEQ} $ 的最大值 $S_{\max} =\dfrac 6{13} t^2=\dfrac {54}{13} $．
所以以 $ QD $ 为腰的等腰 $ \triangle QDE $ 的面积最大值为 $\dfrac{54}{13}$．
由直线 $y=\dfrac 2 3x-\dfrac 4 9$ 解析式可得点 $C\left(\dfrac 2 3,0\right),F\left(0,-\dfrac4 9\right)$，所以 $\tan\angle OFC=\dfrac{OC}{OF}=\dfrac 3 2$．
因为 $DQ\parallel y$ 轴，
所以 $\angle QDH=\angle MFD=\angle OFC$，
所以 $\tan\angle HDQ=\dfrac 3 2$．
不妨记 $DQ=t$，则 $DH=\dfrac2 {\sqrt{13}} t$，$HQ=\dfrac3 {\sqrt{13}} t$．
因为 $\triangle QDE$ 是以 $DQ$ 为等腰的等腰三角形，
① 若 $DQ=DE$ 则 $S_{\triangle DEQ}=\dfrac1 2DE\cdot HQ=\dfrac{3\sqrt{13}}{26} t^2$；
② 若 $DQ=QE$，则 $S_{\triangle DEQ}=\dfrac1 2DE\cdot HQ=\dfrac1 2\times\dfrac4{\sqrt{13}}t\times\dfrac3{\sqrt{13}}t=\dfrac6{13} t^2$．
因为 $\dfrac{3\sqrt{13}}{26} t^2<\dfrac6{13} t^2$
所以当 $DQ=QE$ 时 $\triangle DEQ$ 的面积比 $DQ=DE$ 时大．
设点 $Q\left(x,x^2+2x-3\right)$，则点 $D\left(x,\dfrac2 3 x-\dfrac4 9\right)$．
所以 $DQ=t=\dfrac2 3x-\dfrac 4 9-\left(x^2+2x-3\right)=-x^2-\dfrac4 3 x+\dfrac{23}9$．
所以当 $x=-\dfrac 2 3$ 时，$t_{\max} =3.$
此时 $S_{\triangle DEQ} $ 的最大值 $S_{\max} =\dfrac 6{13} t^2=\dfrac {54}{13} $．
所以以 $ QD $ 为腰的等腰 $ \triangle QDE $ 的面积最大值为 $\dfrac{54}{13}$．
答案
解析
备注
