设 $\omega$ 是一个平面图形，如果用直尺和圆规经过有限步作图（简称尺规作图），画出一个正方形与 $\omega$ 的面积相等（简称等积），那么这样的等积转化称为 $\omega$ 的“化方”．
【难度】
【出处】
无
【标注】
-
阅读填空
如图 1，已知矩形 $ABCD$，延长 $AD$ 到 $E$，使 $DE=DC$，以 $AE$ 为直径作半圆．延长 $CD$ 交半圆于点 $H$，以 $DH$ 为边作正方形 $DFGH$，则正方形 $DFGH$ 与矩形 $ABCD$ 等积．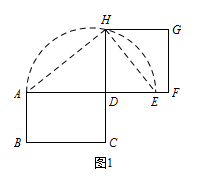
理由：连接 $AH,EH$．
$\because AE$ 为直径，
$\therefore \angle AHE=90^\circ $，
$\therefore \angle HAE+\angle HEA=90^\circ $．
$\because DH\perp AE$，
$\therefore \angle ADH=\angle EDH=90^\circ $．
$\therefore \angle HAD+\angle AHD=90^\circ $，
$\therefore \angle AHD=\angle HED$，
$\therefore \triangle ADH\backsim$
$\therefore \dfrac{AD}{DH}=\dfrac{DH}{DE}$，即 $D{H^2}=AD\cdot DE$．
$\because DE=DC$，
$\therefore D{H^2}=$ -
操作实践
平行四边形的“化方”思路是，先把平行四边形转化为等积的矩形，再把矩形转化为等积的正方形．
如图 2，请作出与平行四边形 $ABCD$ 等积的正方形（不要求写具体作法，保留作图痕迹）．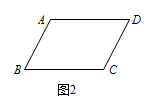
标注答案作图如下：
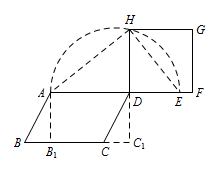解析作法：
① 分别过点 $A,D$ 作直线 $BC$ 的垂线，垂足为点 $B_1,C_1$，
② 延长 $AD$ 至点 $E$，使得 $DE=DC_1$；
③ 以 $AE$ 为直径作半圆；
④ 延长 $C_1D$ 交半圆于点 $H$；
⑤ 以 $DH$ 为边向右作正方形 $DFGH$．
则正方形 $DFGH$ 与平行四边形 $ABCD$ 等积． -
解决问题
三角形的“化方”思路是：先把三角形转化为等积的
如图 3，$\triangle ABC$ 的顶点在正方形网格的格点上，请作出与 $\triangle ABC$ 等积的正方形（不要求写具体作法，保留作图痕迹，不通过计算 $\triangle ABC$ 面积作图）．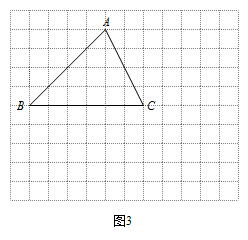
标注答案矩形；作图如下：
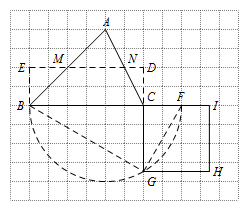解析作法：
① 作 $\triangle ABC$ 的中位线 $MN$，
② 分别过点 $B,C$ 作 $MN$ 的垂线，垂足为点 $E,D$；
③ 延长 $BC$ 至点 $F$，使得 $CF=CD$；
④ 以 $BF$ 为直径作半圆；
⑤ 延长 $DC$ 交半圆于点 $G$；
⑥ 以 $CG$ 为边向右作正方形 $CGHI$．
则正方形 $CGHI$ 与 $\triangle ABC$ 等积． -
拓展探究
$n$ 边形（$n>3$）的“化方”思路之一是：把 $n$ 边形转化为等积的 $n-1$ 边形，$\cdots$，直至转化为等积的三角形，从而可以化方．
如图 4，四边形 $ABCD$ 的顶点在正方形网格的格点上，请作出与四边形 $ABCD$ 等积的正方形（不要求写具体作法，保留作图痕迹，不通过计算四边形 $ABCD$ 面积作图）．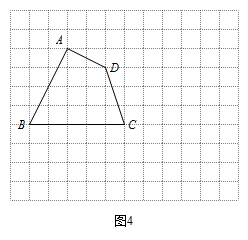
标注答案作图如下：
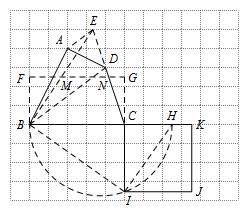解析作法：
① 连接 $BD$，过 $A$ 点作 $AE\parallel BD$ 交 $CD$ 的延长线于点 $E$；
② 作 $\triangle EBC$ 的中位线 $MN$，
③ 分别过点 $B,C$ 作 $MN$ 的垂线，垂足为点 $F,G$；
④ 延长 $BC$ 至点 $H$，使得 $CH=CG$；
⑤ 以 $BH$ 为直径作半圆；
⑥ 延长 $GC$ 交半圆于点 $I$；
⑦ 以 $CI$ 为边向右作正方形 $CIJK$．
则正方形 $CIJK$ 与四边形 $ABCD$ 等积．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
问题4
答案4
解析4
备注4
