若圆 $x^2+y^2 -4x -4y-10=0$ 上至少有三个不同的点到直线 $l:ax+by=0$ 的距离为 $2\sqrt 2$，求直线 $l$ 的倾斜角的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac{\pi}{12},\dfrac{5\pi}{12}\right]$
【解析】
圆的方程即 $C:(x-2)^2+(y-2)^2=18$．
作圆 $O:x^2+y^2=\left(2\sqrt 2\right)^2$，则问题即圆 $O$ 的两条平行的切线与圆 $C$ 有至少 $3$ 个公共点，如图．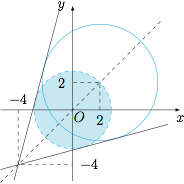
直线 $l$ 倾斜角的取值范围是 $\left[\dfrac{\pi}{4}-\dfrac{\pi}{6},\dfrac{\pi}{4}+\dfrac{\pi}{6}\right]$，即 $\left[\dfrac{\pi}{12},\dfrac{5\pi}{12}\right]$．
作圆 $O:x^2+y^2=\left(2\sqrt 2\right)^2$，则问题即圆 $O$ 的两条平行的切线与圆 $C$ 有至少 $3$ 个公共点，如图．
直线 $l$ 倾斜角的取值范围是 $\left[\dfrac{\pi}{4}-\dfrac{\pi}{6},\dfrac{\pi}{4}+\dfrac{\pi}{6}\right]$，即 $\left[\dfrac{\pi}{12},\dfrac{5\pi}{12}\right]$．
答案
解析
备注
