设 $F_1,F_2$ 分别为椭圆 $\dfrac{x^2}3+y^2=1$ 的左、右焦点，点 $A,B$ 在椭圆上，且 $\overrightarrow{F_1A}=5\overrightarrow{F_2B}$，求 $A$ 点坐标．
【难度】
【出处】
无
【标注】
【答案】
$(0,\pm 1)$
【解析】
如图，延长 $AF_1$ 交椭圆于 $C$，则 $\overrightarrow{AF_1}=5\overrightarrow{F_1C}$．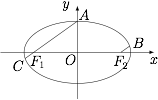
设 $A(x_1,y_1),C(x_2,y_2)$，则根据定比分点坐标公式有 $F_1$ 的坐标$$\left(\dfrac{x_1+5x_2}{6},\dfrac{y_1+5y_2}{6}\right)=(-\sqrt 2,0),$$从而$$x_1+5x_2=-6\sqrt 2,y_1+5y_2=0.$$另一方面，由$$\dfrac{x_1^2}{3}+y_1^2=1,\dfrac{25x_2^2}{3}+25y_2^2=25$$相减可得$$\dfrac{(x_1+5x_2)(x_1-5x_2)}{3}+(y_1+5y_2)(y_1-5y_2)=-24,$$从而可得$$x_1-5x_2=6\sqrt 2.$$因此以上两式相加，可得 $x_1=0$，进而可得 $A=(0,\pm 1)$．
设 $A(x_1,y_1),C(x_2,y_2)$，则根据定比分点坐标公式有 $F_1$ 的坐标$$\left(\dfrac{x_1+5x_2}{6},\dfrac{y_1+5y_2}{6}\right)=(-\sqrt 2,0),$$从而$$x_1+5x_2=-6\sqrt 2,y_1+5y_2=0.$$另一方面，由$$\dfrac{x_1^2}{3}+y_1^2=1,\dfrac{25x_2^2}{3}+25y_2^2=25$$相减可得$$\dfrac{(x_1+5x_2)(x_1-5x_2)}{3}+(y_1+5y_2)(y_1-5y_2)=-24,$$从而可得$$x_1-5x_2=6\sqrt 2.$$因此以上两式相加，可得 $x_1=0$，进而可得 $A=(0,\pm 1)$．
答案
解析
备注
