如图，五边形 $ABOCD$，各顶点坐标为 $A\left(3,4\right),B\left(0,2\right),O(0,0),C\left(4,0\right),D\left(4,2\right)$，请你构造一条经过顶点 $A$ 的直线，将五边形 $ABOCD$ 平分为面积相等的两部分，并求出该直线的解析式．
【难度】
【出处】
无
【标注】
【答案】
直线 $AF$ 解析式为 $y=\dfrac 83x-4$
【解析】
如图，连接 $AO$，作 $BM\parallel AO$ 交 $x$ 轴于点 $M$，连接 $AC$，作 $DN\parallel AC$ 交 $x$ 轴于点 $N$，取 $MN$ 中点 $F$，则直线 $AF$ 将五边形 $ABOCD$ 平分为面积相等的两部分．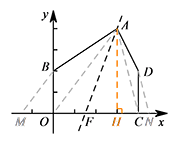
作 $AH\perp x$ 轴于点 $H$，则 $\triangle BMO\backsim \triangle AOH$，
所以 $\dfrac{BO}{MO}=\dfrac{AH}{OH}$，
解得 $OM=1.5$，从而 $M(-1.5,0)$．
同理可得 $CN=0.5$，从而 $N(4.5,0)$．
所以 $F(1.5,0)$．
从而满足条件的直线 $AF$ 解析式为 $y=\dfrac 83x-4$．
作 $AH\perp x$ 轴于点 $H$，则 $\triangle BMO\backsim \triangle AOH$，所以 $\dfrac{BO}{MO}=\dfrac{AH}{OH}$，
解得 $OM=1.5$，从而 $M(-1.5,0)$．
同理可得 $CN=0.5$，从而 $N(4.5,0)$．
所以 $F(1.5,0)$．
从而满足条件的直线 $AF$ 解析式为 $y=\dfrac 83x-4$．
答案
解析
备注
