若把将一个平面图形分成面积相等的两个部分的直线叫做该平面图形的"面线"，其"面线"被该平面图形截得的线段叫做该平面的"面径"（例如圆的直径就是圆的"面径"）．已知等边 $\triangle ABC$ 的边长为 $2$．
【难度】
【出处】
无
【标注】
-
如图，$D$ 为 $BC$ 的中点，连接 $AD$，$M$ 为 $AB$ 上的一点且 $0<AM<1$，$E$ 是 $DC$ 上一点，连接 $ME$ 交 $AD$ 于点 $O$，且 $S_{\triangle MOA}=S_{\triangle DOE}$．求证：$ME$ 是 $\triangle ABC$ 的面径；标注答案略解析因为 $S_{\triangle MOA}=S_{\triangle DOE}$，
所以 $S_{四边形BMOD}+S_{\triangle DOE}=S_{四边形BMOD}+S_{\triangle MOA}$，
所以 $S_{\triangle BME}=S_{\triangle ABD}=\dfrac 12 S_{\triangle ABC}$，
即 $ME$ 是 $\triangle ABC$ 的面径． -
试求等边 $\triangle ABC$ 面径长 $l$ 的取值范围．标注答案等边 $\triangle ABC$ 面径长 $l$ 的取值范围为 $\sqrt 2\leqslant l\leqslant \sqrt 3$解析由 $(1)$ 可得 $S_{\triangle MAE}=S_{\triangle DAE}$，
所以 $MD\parallel AE$，
从而 $\dfrac{BM}{MA}=\dfrac{BD}{DE}$．
如图，作 $MF\perp BC$ 于点 $F$．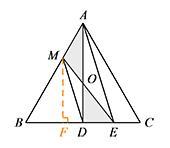
令 $BM=2x$，则 $AM=2-2x$，$BF=x$，$MF=\sqrt 3x$，
所以 $DF=1-x$，$DE=\dfrac 1x-1$．
由勾股定理可得 $l^2=MF^2+EF^2=3x^2+\left(\dfrac 1x-x\right)^2=\left(2x+\dfrac 1x\right)^2-6$．
因为 $2x+\dfrac 1x\geqslant 2\sqrt{2x\cdot \dfrac 1x}=2\sqrt 2$，
所以 $l^2\geqslant 2$．
而 $l\leqslant AD=\sqrt 3$，
所以 $\sqrt 2\leqslant l\leqslant \sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
