如图，在平面直角坐标系中，抛物线 $y=\dfrac 12x^2-3x-8$ 与 $x$ 轴交于 $A,B$ 两点，与 $y$ 轴交于点 $C$，直线 $l$ 经过原点 $O$，与抛物线的一个交点为 $D$，与抛物线的对称轴交于点 $E\left(3,-4\right)$，连接 $CE$．若点 $P$ 是 $y$ 轴负半轴上的一个动点，设其坐标为 $\left(0,m\right)$，直线 $PB$ 与直线 $l$ 交于点 $Q$．试探究：当 $m$ 为何值时，$\triangle OPQ$ 是等腰三角形．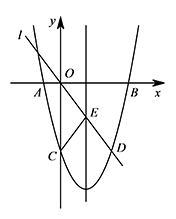
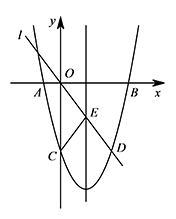
【难度】
【出处】
无
【标注】
【答案】
当 $m$ 的值为 $-\dfrac 83$ 或 $-\dfrac{32}3$ 时，$\triangle OPQ$ 是等腰三角形
【解析】
由抛物线 $y=\dfrac 12x^2-3x-8=\dfrac 12(x-8)(x+2)$，
可得点 $A,B,C$ 的坐标分别为 $(-2,0),(8,0),(0,-8)$．
所以 $CE=\sqrt{(3-0)^2+(-4+8)^2}=5=OE$，
所以 $\triangle OEC$ 是顶角为钝角的等腰三角形，即 $\angle OEC>90^\circ$．
$\triangle OPQ$ 为等腰三角形有三种可能：
① 当 $PO=PQ$ 时，即 $\angle OPQ$ 为顶角．
显然 $\angle POQ=\angle COE$，
所以 $\angle OPQ=\angle OEC>90^\circ$，
由题意可知这种可能不存在；
② 当 $OP=OQ$ 时，则 $\angle OPQ=\angle OQP$．
如图，过点 $E$ 作 $PQ$ 的平行线，分别交 $x,y$ 轴于点 $F,G$．
则 $\angle OGE=\angle OPQ=\angle OQP=\angle OEG$，
所以 $OG=OE=5$，即点 $G$ 的坐标为 $(0,-5)$，
所以直线 $GE$ 的解析式为 $y=\dfrac 13x-5$，
所以点 $F$ 的坐标为 $(15,0)$．
而 $\dfrac{OP}{OG}=\dfrac{OB}{OF}$，
所以 $\dfrac{-m}{5}=\dfrac{8}{15}$，即 $m=-\dfrac 83$；
③ 当 $QO=QP$ 时，则 $\angle QPO=\angle QOP=\angle OCE$，
所以 $CE\parallel PQ$．
如图，设直线 $CE$ 与 $x$ 轴交于点 $H$．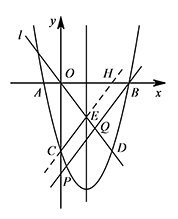
由 $C,E$ 点坐标可得直线 $CE$ 的解析式为 $y=\dfrac 43x-8$，
所以点 $H$ 的坐标为 $(6,0)$．
而 $\dfrac{OC}{OP}=\dfrac{OH}{OB}$，
所以 $\dfrac{8}{-m}=\dfrac{6}{8}$，即 $m=-\dfrac{32}3$．
综上可得，当 $m$ 的值为 $-\dfrac 83$ 或 $-\dfrac{32}3$ 时，$\triangle OPQ$ 是等腰三角形．
可得点 $A,B,C$ 的坐标分别为 $(-2,0),(8,0),(0,-8)$．
所以 $CE=\sqrt{(3-0)^2+(-4+8)^2}=5=OE$，
所以 $\triangle OEC$ 是顶角为钝角的等腰三角形，即 $\angle OEC>90^\circ$．
$\triangle OPQ$ 为等腰三角形有三种可能：
① 当 $PO=PQ$ 时，即 $\angle OPQ$ 为顶角．
显然 $\angle POQ=\angle COE$，
所以 $\angle OPQ=\angle OEC>90^\circ$，
由题意可知这种可能不存在；
② 当 $OP=OQ$ 时，则 $\angle OPQ=\angle OQP$．
如图，过点 $E$ 作 $PQ$ 的平行线，分别交 $x,y$ 轴于点 $F,G$．
则 $\angle OGE=\angle OPQ=\angle OQP=\angle OEG$，所以 $OG=OE=5$，即点 $G$ 的坐标为 $(0,-5)$，
所以直线 $GE$ 的解析式为 $y=\dfrac 13x-5$，
所以点 $F$ 的坐标为 $(15,0)$．
而 $\dfrac{OP}{OG}=\dfrac{OB}{OF}$，
所以 $\dfrac{-m}{5}=\dfrac{8}{15}$，即 $m=-\dfrac 83$；
③ 当 $QO=QP$ 时，则 $\angle QPO=\angle QOP=\angle OCE$，
所以 $CE\parallel PQ$．
如图，设直线 $CE$ 与 $x$ 轴交于点 $H$．
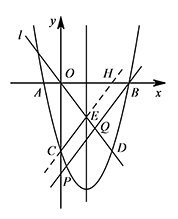由 $C,E$ 点坐标可得直线 $CE$ 的解析式为 $y=\dfrac 43x-8$，所以点 $H$ 的坐标为 $(6,0)$．
而 $\dfrac{OC}{OP}=\dfrac{OH}{OB}$，
所以 $\dfrac{8}{-m}=\dfrac{6}{8}$，即 $m=-\dfrac{32}3$．
综上可得，当 $m$ 的值为 $-\dfrac 83$ 或 $-\dfrac{32}3$ 时，$\triangle OPQ$ 是等腰三角形．
答案
解析
备注
