如图，已知抛物线 $y=x^2-2x-3$ 经过 $A\left(-1,0\right)$，$B\left(3,0\right)$，$ C\left(0,﹣3\right)$ 三点，直线 $l$ 是抛物线的对称轴．点 $M$ 是直线 $l$ 上的动点，且 $\triangle MAC$ 为等腰三角形，请直接写出所有符合条件的点 $M$ 的坐标．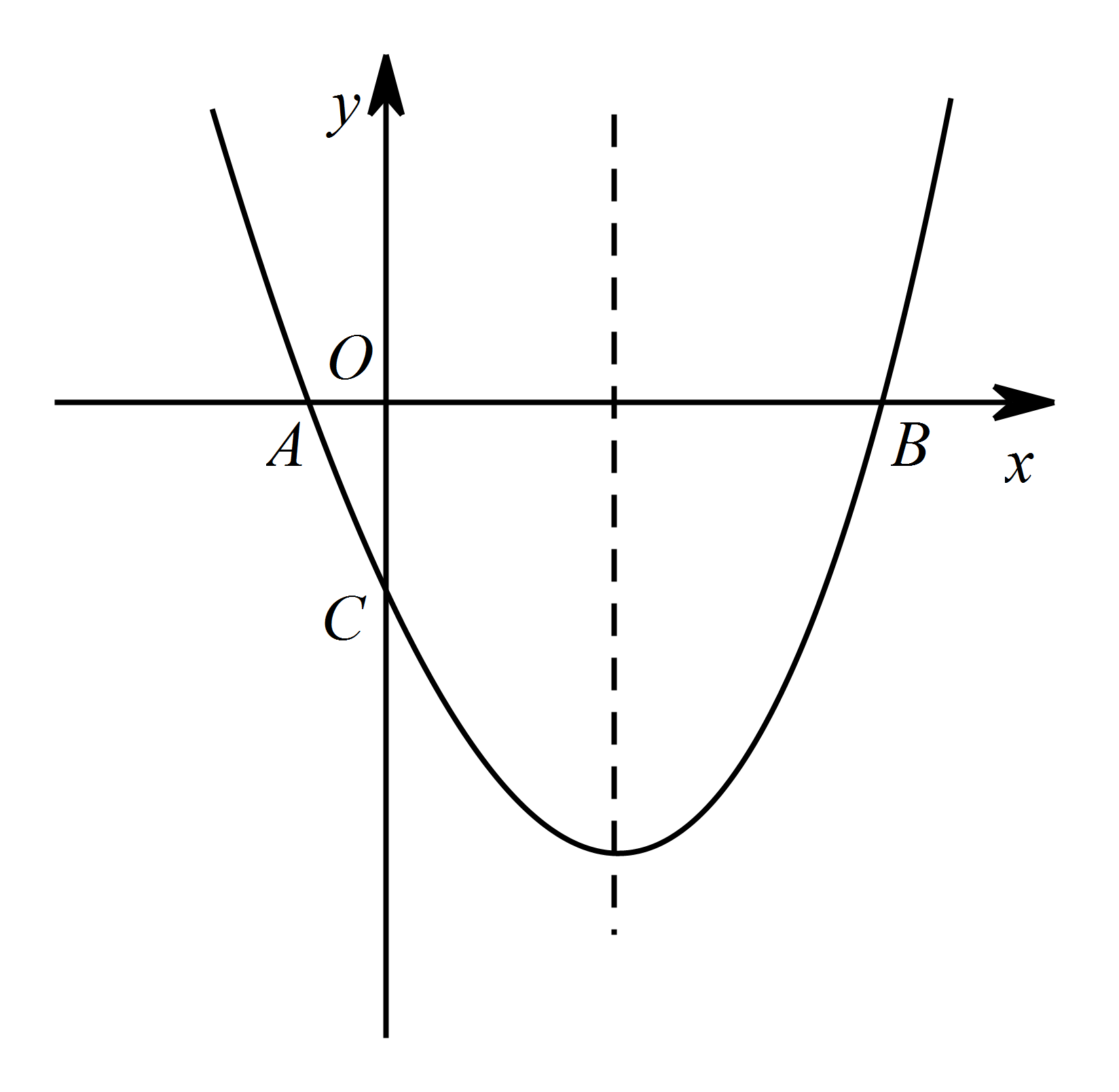
【难度】
【出处】
无
【标注】
【答案】
符合条件的点 $M$ 的坐标为 $ M\left(1,\sqrt{6}\right)$ $ \left(1,-\sqrt{6} \right)$ $ \left(1,-1\right)$ $ \left(1,0\right)$
【解析】
如图，抛物线的对称轴为 $x=-\dfrac{b}{2a} =1$．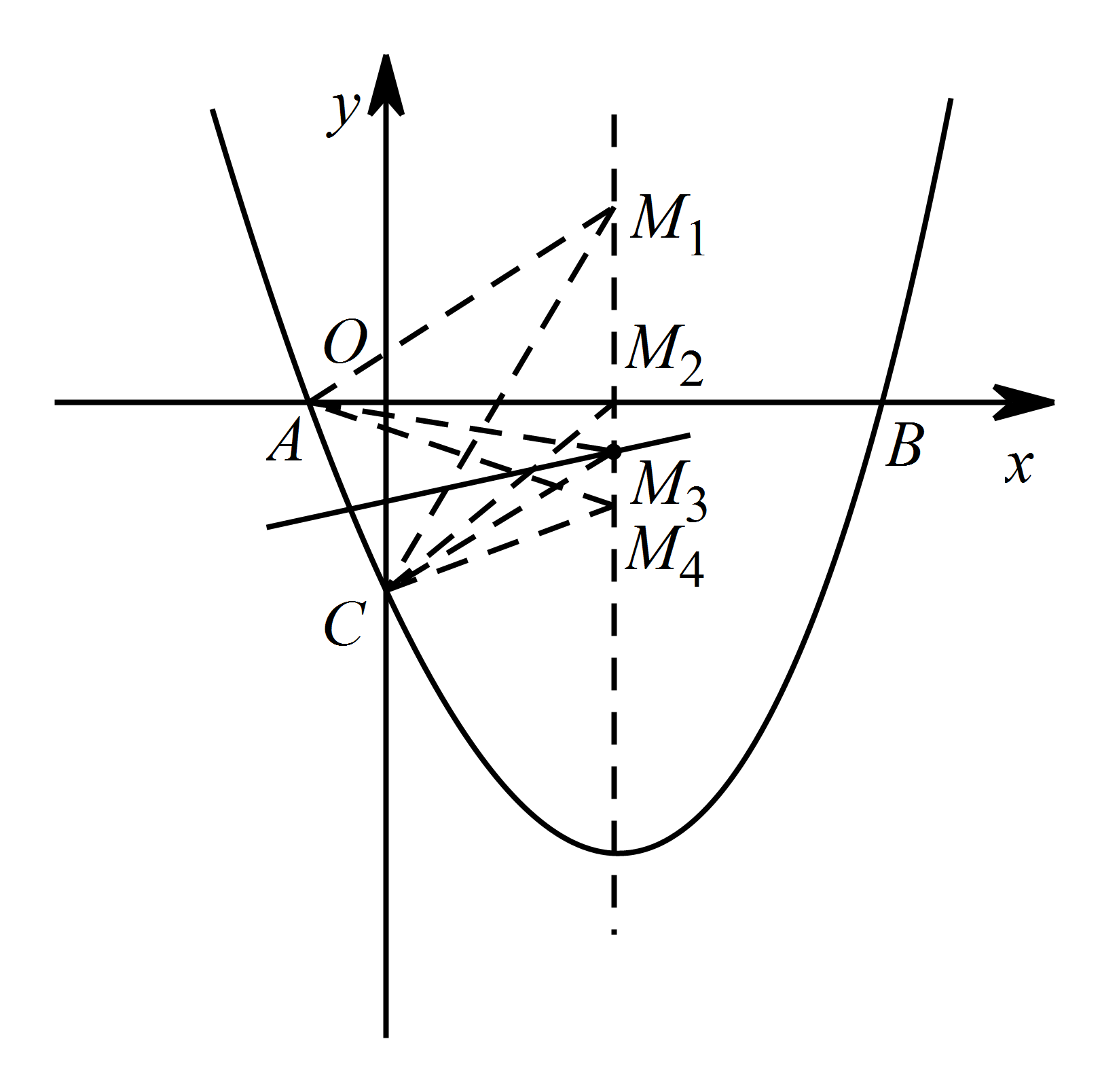
设点 $M$ 的坐标为 $\left(1,m\right)$，已知点 $A\left(-1,0\right)$，点 $C\left(0,-3\right)$，
则 $MA^2=m^2+4$，$MC^2=\left(3+m\right)^2+1=m^2+6m+10$，$AC^2=10$．
① 若 $MA=MC$，则有 $m^2+4=m^2+6m+10$，
解得 $m=-1$，
② 若 $MA=AC$，则有 $m^2+4=10$，
解得 $m=\pm\sqrt{6} $；
③ 若 $MC=AC$，则有 $m^2+6m+10=10$，
解得 $m_1=0$，$m_2=-6$．
当 $m=-6$ 时，$M,A,C $ 三点共线，构不成三角 形，不合题意，故舍去．
综上可知，符合条件的点 $M$ 的坐标为 $ M\left(1,\sqrt{6}\right)$ $ \left(1,-\sqrt{6} \right)$ $ \left(1,-1\right)$ $ \left(1,0\right)$．
设点 $M$ 的坐标为 $\left(1,m\right)$，已知点 $A\left(-1,0\right)$，点 $C\left(0,-3\right)$，则 $MA^2=m^2+4$，$MC^2=\left(3+m\right)^2+1=m^2+6m+10$，$AC^2=10$．
① 若 $MA=MC$，则有 $m^2+4=m^2+6m+10$，
解得 $m=-1$，
② 若 $MA=AC$，则有 $m^2+4=10$，
解得 $m=\pm\sqrt{6} $；
③ 若 $MC=AC$，则有 $m^2+6m+10=10$，
解得 $m_1=0$，$m_2=-6$．
当 $m=-6$ 时，$M,A,C $ 三点共线，构不成三角 形，不合题意，故舍去．
综上可知，符合条件的点 $M$ 的坐标为 $ M\left(1,\sqrt{6}\right)$ $ \left(1,-\sqrt{6} \right)$ $ \left(1,-1\right)$ $ \left(1,0\right)$．
答案
解析
备注
