如图，点 $P(2,n)$ 在函数 $y=\dfrac 43x(x\geqslant 0)$ 的图象 $OL$ 与 $x$ 轴正半轴夹角的平分线上．请在 $OL$、$x$ 轴上分别找点 $E,F$，使 $\triangle PEF$ 的周长最小，简要叙述作图方法，并求出周长的最小值．
【难度】
【出处】
无
【标注】
【答案】
$\triangle PEF$ 周长的最小值为 $\dfrac{8\sqrt 5}5$
【解析】
如图，过点 $P$ 作 $x$ 轴、$OL$ 的垂线，垂足分别为点 $M,N$．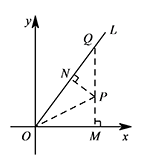
延长 $MP$ 交 $OL$ 于点 $Q$，则点 $Q$ 的坐标为 $\left(2,\dfrac 83\right)$，
所以 $OM=2,MQ=\dfrac 83$，从而 $OQ=\sqrt{OM^2+MQ^2}=\dfrac{10}3$．
由题意可得 $PN=PM=n$，所以 $PQ=\dfrac 83-n$．
易证 $\triangle QMO\backsim \triangle QNP$，
所以 $\dfrac{PQ}{OQ}=\dfrac{PN}{OM}$，
即 $\dfrac{\dfrac 83-n}{\dfrac{10}3}=\dfrac{n}{2}$，解得 $n=1$，
所以点 $P$ 的坐标为 $(2,1)$，$OP=\sqrt 5$．
作点 $P$ 关于 $OL$、$x$ 轴的对称点 $P_1,P_2$，连接 $P_1P_2$，与 $OL$、$x$ 轴的交点即为所求点 $E,F$．此时 $\triangle PEF$ 的周长最小，最小值即为 $P_1P_2$ 的长．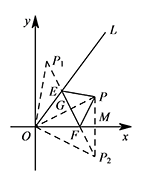
连接 $OP_1,OP_2$，则 $\angle P_1OE=\angle POE=\angle POF=\angle P_2OF$，
所以 $OP$ 平分 $\angle P_1OP_2$．
而 $OP_1=OP=OP_2$，所以 $OP\perp P_1P_2$．
记 $OP$ 与 $P_1P_2$ 的交点为 $G$，则 $P_1P_2=2GP_2$．
连接 $PP_1$，则 $PP_1=2PM=2$．
由 $S_{\triangle OPP_2}=\dfrac 12OM\cdot PP_2=\dfrac 12OP\cdot P_2G$，
得到 $P_2G=\dfrac{4}{\sqrt 5}=\dfrac{4\sqrt 5}5$，
所以 $P_1P_2=2P_2G=\dfrac{8\sqrt 5}5$．
故 $\triangle PEF$ 周长的最小值为 $\dfrac{8\sqrt 5}5$．
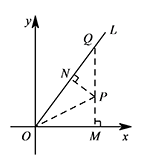延长 $MP$ 交 $OL$ 于点 $Q$，则点 $Q$ 的坐标为 $\left(2,\dfrac 83\right)$，所以 $OM=2,MQ=\dfrac 83$，从而 $OQ=\sqrt{OM^2+MQ^2}=\dfrac{10}3$．
由题意可得 $PN=PM=n$，所以 $PQ=\dfrac 83-n$．
易证 $\triangle QMO\backsim \triangle QNP$，
所以 $\dfrac{PQ}{OQ}=\dfrac{PN}{OM}$，
即 $\dfrac{\dfrac 83-n}{\dfrac{10}3}=\dfrac{n}{2}$，解得 $n=1$，
所以点 $P$ 的坐标为 $(2,1)$，$OP=\sqrt 5$．
作点 $P$ 关于 $OL$、$x$ 轴的对称点 $P_1,P_2$，连接 $P_1P_2$，与 $OL$、$x$ 轴的交点即为所求点 $E,F$．此时 $\triangle PEF$ 的周长最小，最小值即为 $P_1P_2$ 的长．
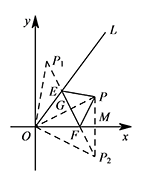连接 $OP_1,OP_2$，则 $\angle P_1OE=\angle POE=\angle POF=\angle P_2OF$，所以 $OP$ 平分 $\angle P_1OP_2$．
而 $OP_1=OP=OP_2$，所以 $OP\perp P_1P_2$．
记 $OP$ 与 $P_1P_2$ 的交点为 $G$，则 $P_1P_2=2GP_2$．
连接 $PP_1$，则 $PP_1=2PM=2$．
由 $S_{\triangle OPP_2}=\dfrac 12OM\cdot PP_2=\dfrac 12OP\cdot P_2G$，
得到 $P_2G=\dfrac{4}{\sqrt 5}=\dfrac{4\sqrt 5}5$，
所以 $P_1P_2=2P_2G=\dfrac{8\sqrt 5}5$．
故 $\triangle PEF$ 周长的最小值为 $\dfrac{8\sqrt 5}5$．
答案
解析
备注
