如图1，等边 $\triangle ABC$ 的边长为 $6$，$AD,BE$ 是两条边上的高，点 $O$ 为其交点．$P,N$ 分别是 $BE,BC$ 上的动点．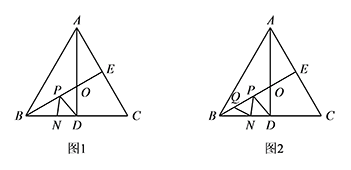
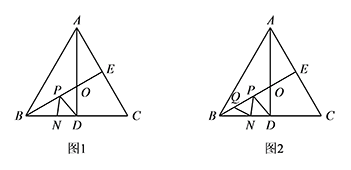
【难度】
【出处】
无
【标注】
-
当 $PN+PD$ 的长度取得最小值时，求 $BP$ 的长度；标注答案$BP=\sqrt 3$解析由等边三角形轴对称的性质可得，点 $D$ 关于 $BE$ 的对称点 $D'$ 在 $AB$ 上，且为 $AB$ 的中点．
连接 $PD'$，则 $PD'=PD$．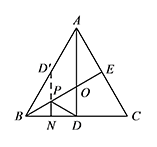
过点 $D'$ 作 $BC$ 的垂线，垂足为点 $N$，交 $BE$ 于点 $P$，
此时 $D'N$ 即为 $PN+PD$ 长度的最小值．
显然 $D'N\parallel AD$，即点 $N$ 为 $BD$ 的中点．
所以 $BN=\dfrac 14BC=\dfrac 32$，
从而 $BP=\dfrac{BN}{\cos \angle PBN}=\sqrt 3$． -
如图2，若点 $Q$ 在线段 $BO$ 上，$BQ=1$，求 $QN+NP+PD$ 的最小值．标注答案最小值为 $\sqrt{10}$解析作点 $Q$ 关于 $BC$ 的对称点 $Q'$，则 $BQ'=1$，$\angle CBQ'=30^\circ$．
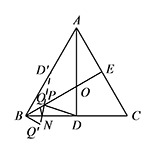$D'$ 是点 $D$ 关于 $BE$ 的对称点，连接 $D'Q'$，交 $BE$ 于点 $P$，交 $BC$ 于点 $N$，
此时 $D'Q'$ 即为 $QN+NP+PD$ 的最小值．
显然 $\angle D'BQ'=90^\circ$，
所以 $D'Q'=\sqrt{BD'^2+BQ'^2}=\sqrt{10}$，
即 $QN+NP+PD$ 的最小值为 $\sqrt{10}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
