设二次函数 $y=x^2+2ax+\dfrac {a^2}{2}$（$a<0$）的图象顶点为 $A$，与 $x$ 轴交点为 $B,C$．
【难度】
【出处】
无
【标注】
-
当 $\triangle {ABC}$ 为等边三角形时，求 $a$ 的值；标注答案$a=-\sqrt 6$解析由 $y=x^2+2ax+\dfrac{a^2}{2}=(x+a)^2-\dfrac{a^2}2$，可得 $A\left(-a,-\dfrac{a^2}2\right)$．
令 $y=0$，则 $(x+a)^2-\dfrac{a^2}2=0$，
解得 $x=-a\pm \dfrac{\sqrt 2}2a$．
如图，过点 $A$ 作 $AD\perp BC$ 于点 $D$，则 $AD=\dfrac{a^2}2$，$BD=-\dfrac{\sqrt 2}2a$．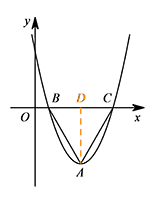
因为 $\triangle ABC$ 为等边三角形，所以 $AD=\sqrt 3 BD$，
从而 $\dfrac{a^2}2=-\sqrt 3\times \dfrac{\sqrt 2}2a$，
解得 $a=-\sqrt 6$． -
当 $\triangle {ABC}$ 为等腰直角三角形时，求 $a$ 的值．标注答案$a=-\sqrt 2$解析同第1问可得，$AD=\dfrac{a^2}2$，$BD=-\dfrac{\sqrt 2}2a$．
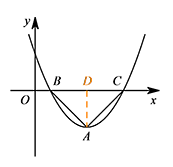因为 $\triangle ABC$ 为等腰直角三角形，所以 $AD=BD$，
从而 $\dfrac{a^2}2=-\dfrac{\sqrt 2}2a$，
解得 $a=-\sqrt 2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
