已知抛物线 $y=a\left(x-1\right)^2-3\left(a\neq 0\right)$ 的图象与 $y$ 轴交于点 $A\left(0,-2\right)$，顶点为 $B$．在 $x$ 轴上求一点 $P$，使得 $\triangle PAB$ 的周长取最小值．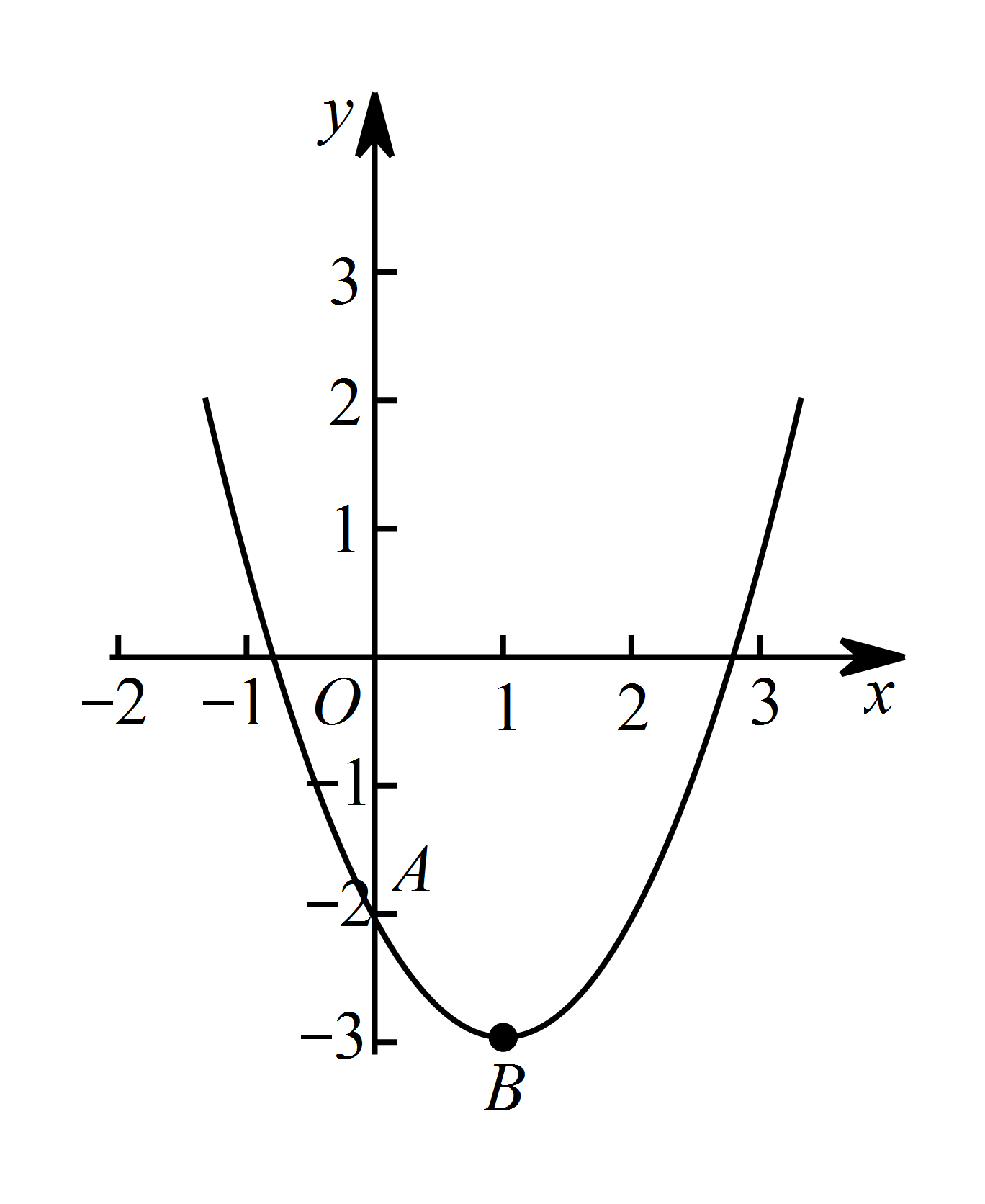
【难度】
【出处】
无
【标注】
【答案】
把 $A\left(0,-2\right)$ 代入 $y=a\left(x-1\right)^2-3$ 得 $-2=a\left(0-1\right)^2-3$，
解得 $a=1$．
因为顶点为 $B$，所以 $ B\left(1,-3\right)$．
设 $A\left(0,-2\right)$ 点关于 $x$ 轴的对称点记作 $E$，则 $E\left(0,2\right)$．
如图，连接 $EB$ 交 $x$ 轴于点 $P$，则 $P$ 点即为所求．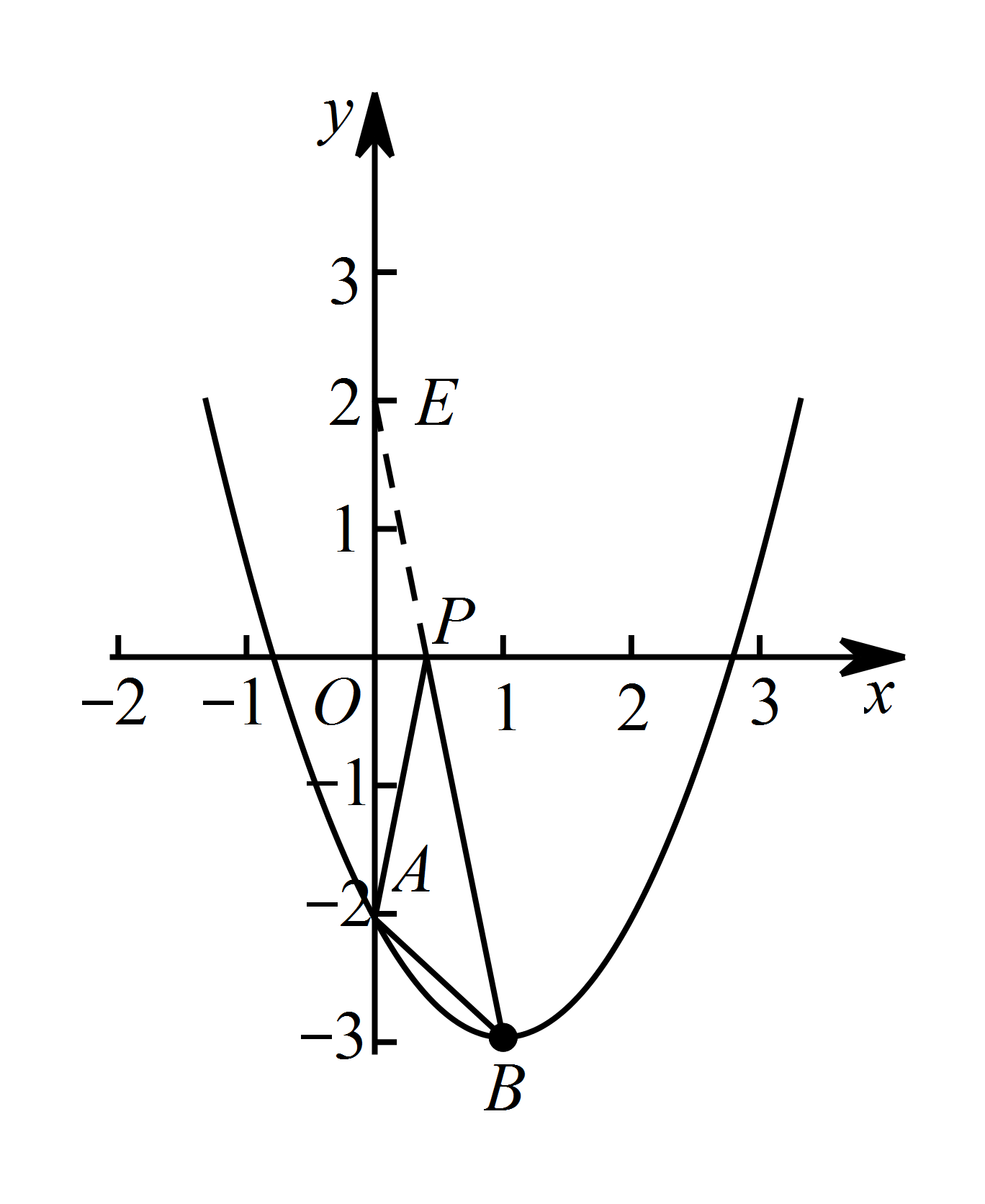
因为 $ PA+PB=PE+PB\leqslant EB$，
所以 $ E$，$P$，$B$ 三点在同一条直线上时，$ PA+PB $ 取得最小值．
由于过 $E$，$B$ 点的一次函数解析式为 $y=-5x+2$．
当 $y=0$ 时，$x=\dfrac{2}{5 }$．
所以 $ P\left(\dfrac{2}{ 5},0\right) $
解得 $a=1$．
因为顶点为 $B$，所以 $ B\left(1,-3\right)$．
设 $A\left(0,-2\right)$ 点关于 $x$ 轴的对称点记作 $E$，则 $E\left(0,2\right)$．
如图，连接 $EB$ 交 $x$ 轴于点 $P$，则 $P$ 点即为所求．
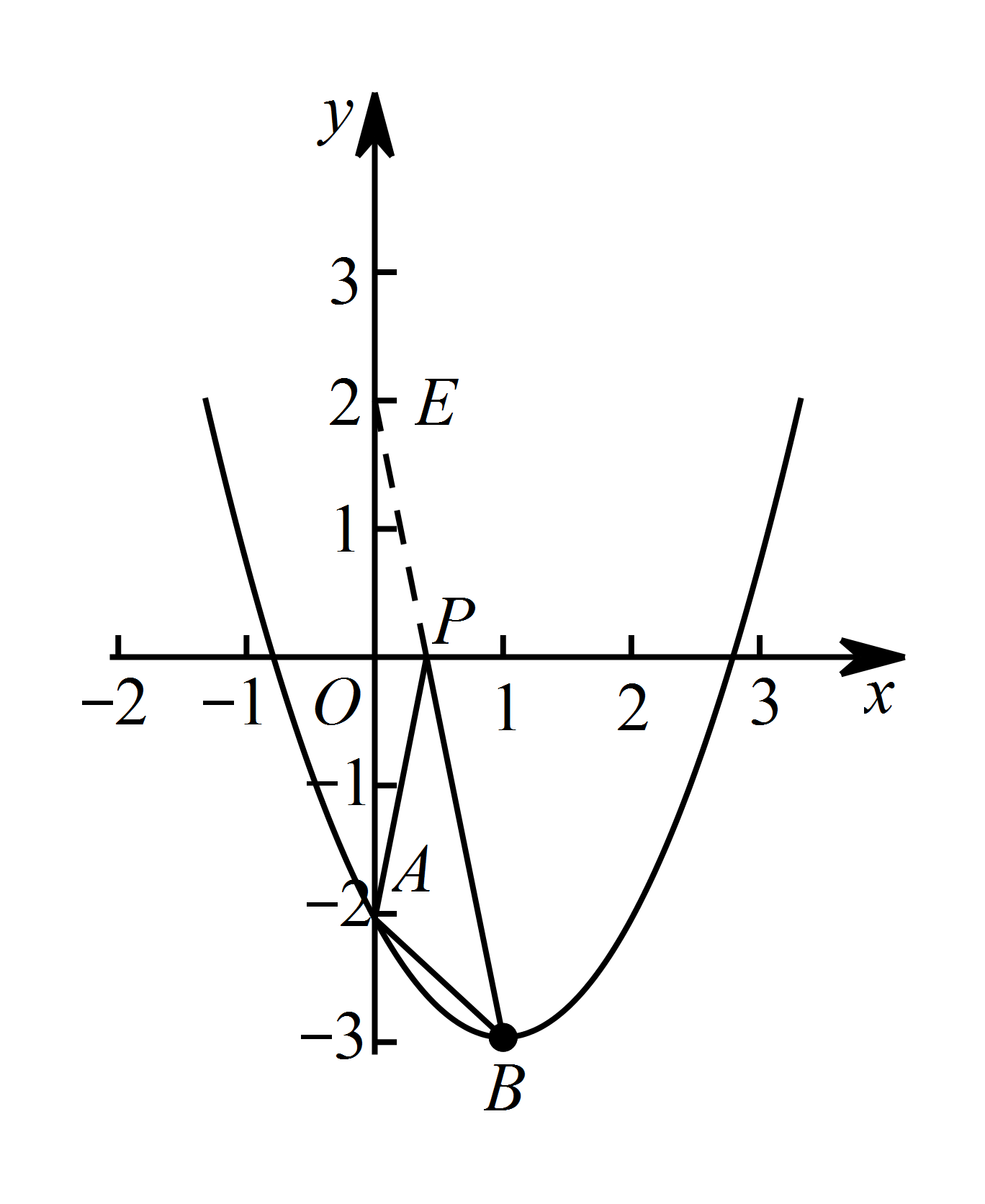因为 $ PA+PB=PE+PB\leqslant EB$，所以 $ E$，$P$，$B$ 三点在同一条直线上时，$ PA+PB $ 取得最小值．
由于过 $E$，$B$ 点的一次函数解析式为 $y=-5x+2$．
当 $y=0$ 时，$x=\dfrac{2}{5 }$．
所以 $ P\left(\dfrac{2}{ 5},0\right) $
【解析】
略
答案
解析
备注
