如图，在 $\mathrm {Rt}\triangle ABC$ 中，$\angle ACB=90^\circ$，$AC=6$，$BC=8$，点 $D$ 以每秒 $1$ 个单位长度的速度由点 $A$ 向点 $B$ 匀速运动，到达 $B$ 点即停止运动，$M,N$ 分别是 $AD,CD$ 的中点，连接 $MN$，设点 $D$ 运动的时间为 $t$．若 $\triangle DMN$ 是等腰三角形，求 $t$ 的值．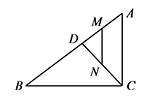
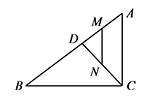
【难度】
【出处】
无
【标注】
【答案】
当 $t=5$ 或 $6$ 或 $\dfrac{36}5$ 时，$\triangle DMN$ 为等腰三角形
【解析】
由已知可得 $DM=\dfrac 12AD$，$DN=\dfrac 12CD$，$MN=\dfrac 12AC=3$，$AB=10$．
对 $\triangle PDE$ 是等腰三角形进行分类讨论：
① 当 $MD=MN=3$ 时，可得 $AD=AC=6$，
所以 $t=6$．
② 当 $DM=DN$ 时，则 $AD=DC$，
所以点 $D$ 是 $AB$ 的中点，即 $AD=\dfrac 12 AB=5$，
所以 $t=5$．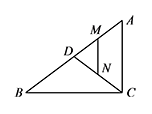
③ 当 $DN=MN=3$ 时，则 $AC=DC$．
连接 $MC$，则 $CM\perp AD$．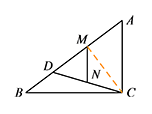
由 $\cos A=\dfrac{AM}{AC}=\dfrac{AC}{AB}$，
可得 $AM=\dfrac{18}5$，
即 $AD=2AM=\dfrac{36}5$，
所以 $t=\dfrac{36}5.$
综上可得，当 $t=5$ 或 $6$ 或 $\dfrac{36}5$ 时，$\triangle DMN$ 为等腰三角形．
对 $\triangle PDE$ 是等腰三角形进行分类讨论：
① 当 $MD=MN=3$ 时，可得 $AD=AC=6$，
所以 $t=6$．
② 当 $DM=DN$ 时，则 $AD=DC$，所以点 $D$ 是 $AB$ 的中点，即 $AD=\dfrac 12 AB=5$，
所以 $t=5$．
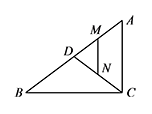③ 当 $DN=MN=3$ 时，则 $AC=DC$．连接 $MC$，则 $CM\perp AD$．
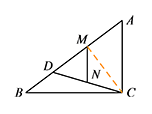由 $\cos A=\dfrac{AM}{AC}=\dfrac{AC}{AB}$，可得 $AM=\dfrac{18}5$，
即 $AD=2AM=\dfrac{36}5$，
所以 $t=\dfrac{36}5.$
综上可得，当 $t=5$ 或 $6$ 或 $\dfrac{36}5$ 时，$\triangle DMN$ 为等腰三角形．
答案
解析
备注
