如图,直线 $y=5x+5$ 交 $x$ 轴于点 $A$,交 $y$ 轴于点 $C$,过 $A$,$C$ 两点的二次函数 $y=-x^2+4x+5$ 的图象交 $x$ 轴于另一点 $B$.若点 $H$ 为二次函数 图象的顶点,点 $M\left(4,m\right)$ 是该二次函数图象上一点,在 $x$ 轴、$y$ 轴上分别找点 $F,E$,使四边形 $HEFM$ 的周长最小,求出点 $F,E$ 的坐标.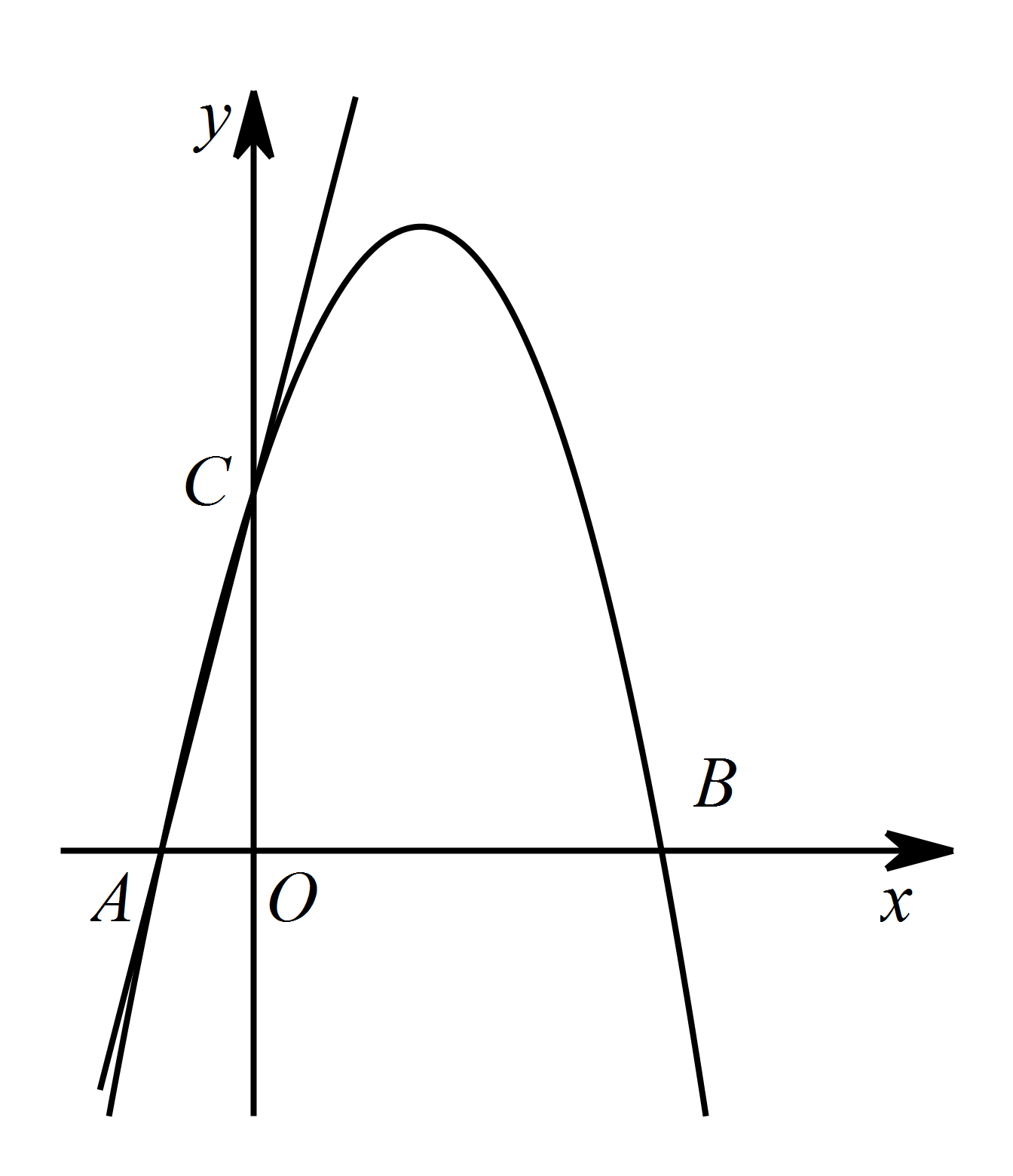

【难度】
【出处】
无
【标注】
【答案】
点 $F$,$E$ 的坐标分别为 $F\left(\dfrac{13}{7},0\right)$,$E\left(0,\dfrac{13}{3}\right)$
【解析】
由题意可得二次函数的顶点坐标为 $H\left(2,9\right)$,点 $M$ 的坐标为 $M\left(4,5\right)$,
作点 $H\left(2,9\right)$ 关于 $y$ 轴的对称点 $H_1$,则点 $H_1$ 的坐标为 $H_1\left(-2,9\right)$,
作点 $M\left(4,5\right)$ 关于 $x$ 轴的对称点 $M_1$,则点 $M_1$ 的坐标为 $M_1\left(4,-5\right)$,
连接 $H_1M_1$ 分别交 $x$ 轴于点 $F$,$y$ 轴于点 $E$.
所以 $H_1M_1+HM$ 的长度是四边形 $HEFM$ 的最小周长,则点 $F,E$ 即为所求.
设直线 $H_1M_1$ 的函数表达式为 $y=k_1x+b_1$,
直线 $H_1M_1$ 过点 $M_1\left(4,-5\right)$,$H_1\left(-2,9\right)$,
根据题意得方程组 $\begin{cases}-5=4k_1+b_1,\\ 9=-k_1+b_1.\end{cases}$
解得 $\begin{cases} k_1=-\dfrac{7}{3},\\ b_1=\dfrac{13}{3}.\end{cases}$
所以 $y=-\dfrac{7}{3}x+\dfrac{13}{3}$,
所以点 $F,E$ 的坐标分别为 $F\left(\dfrac{13}{7},0\right)$,$E\left(0,\dfrac{13}{3}\right)$.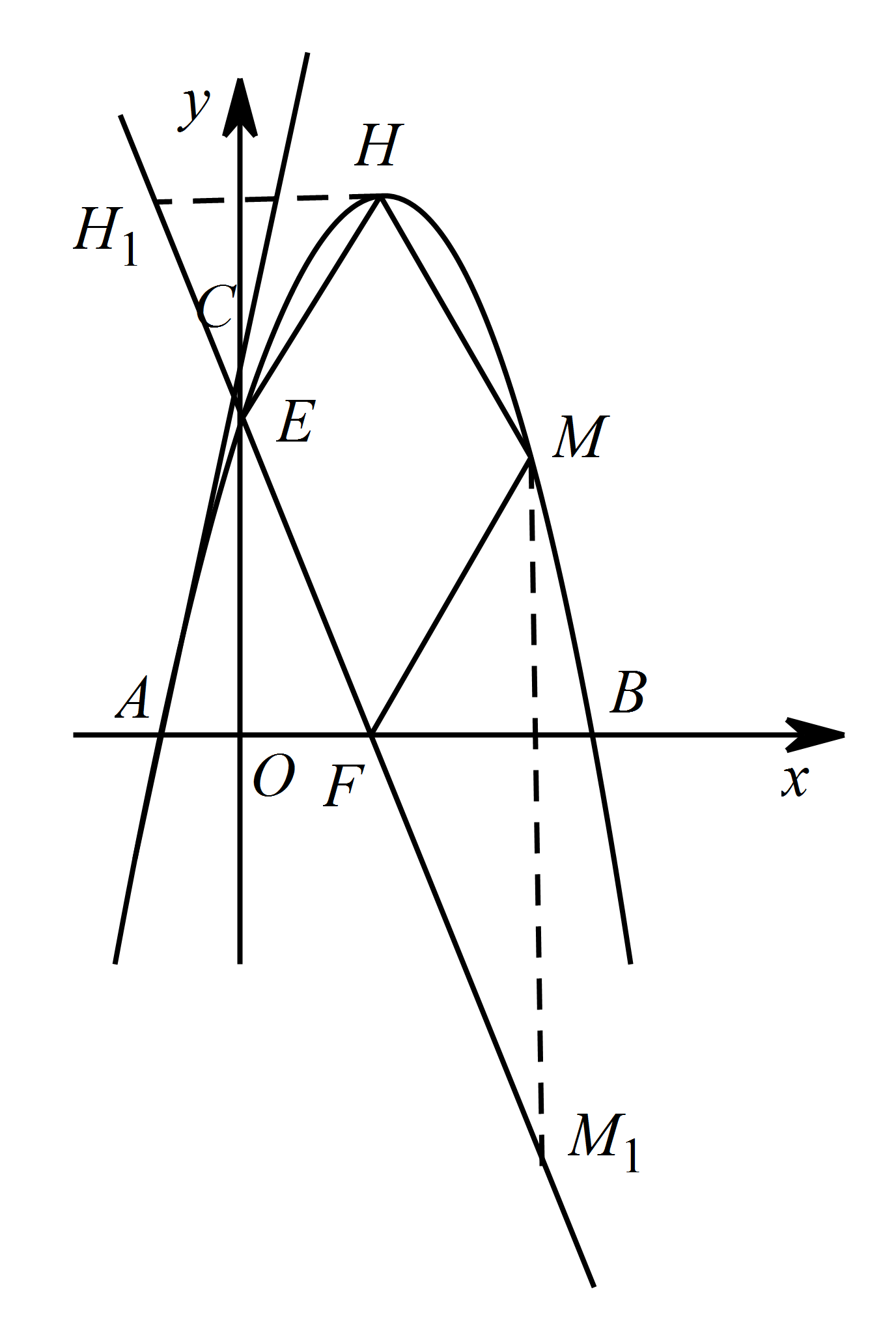
作点 $H\left(2,9\right)$ 关于 $y$ 轴的对称点 $H_1$,则点 $H_1$ 的坐标为 $H_1\left(-2,9\right)$,
作点 $M\left(4,5\right)$ 关于 $x$ 轴的对称点 $M_1$,则点 $M_1$ 的坐标为 $M_1\left(4,-5\right)$,
连接 $H_1M_1$ 分别交 $x$ 轴于点 $F$,$y$ 轴于点 $E$.
所以 $H_1M_1+HM$ 的长度是四边形 $HEFM$ 的最小周长,则点 $F,E$ 即为所求.
设直线 $H_1M_1$ 的函数表达式为 $y=k_1x+b_1$,
直线 $H_1M_1$ 过点 $M_1\left(4,-5\right)$,$H_1\left(-2,9\right)$,
根据题意得方程组 $\begin{cases}-5=4k_1+b_1,\\ 9=-k_1+b_1.\end{cases}$
解得 $\begin{cases} k_1=-\dfrac{7}{3},\\ b_1=\dfrac{13}{3}.\end{cases}$
所以 $y=-\dfrac{7}{3}x+\dfrac{13}{3}$,
所以点 $F,E$ 的坐标分别为 $F\left(\dfrac{13}{7},0\right)$,$E\left(0,\dfrac{13}{3}\right)$.

答案
解析
备注