如图，在平面直角坐标系中，矩形 $OABC$ 的边 $OA$ 在 $y$ 轴的正半轴上，$OC$ 在 $x$ 轴的正半轴上，$\angle AOC$ 的平分线交 $AB$ 于点 $D$，$E$ 为 $BC$ 的中点，已知 $A\left(0,4\right)$，$C\left(5,0\right)$，二次函数 $y=\dfrac45x^2+bx+c$ 的图象抛物线经过 $A,C$ 两点．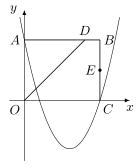
【难度】
【出处】
无
【标注】
-
$F,G$ 分别为 $x$ 轴，$y$ 轴上的动点，顺次连接 $D,E,F,G$ 构成四边形 $DEFG$，求四边形 $DEFG$ 周长的最小值；标注答案$\sqrt{117}+\sqrt5$解析将 $A\left(0,4\right)$，$C\left(5,0\right)$ 代入二次函数 $y=\dfrac45 x^2+bx+c$，
得 $\begin{cases}20+5b+c=0,\\c=4,\end{cases}$
解得 $\begin{cases}b=-\dfrac{24}{5},\\c=4.\end{cases}$
故二次函数的表达式 $y=\dfrac45 x^2-\dfrac{24}{5} x+4$．
如图：
延长 $EC$ 至 $E'$，使 $E'C=EC$，
延长 $DA$ 至 $D'$，使 $D'A=DA$，
连接 $D'E'$，交 $x$ 轴于 $F$ 点，交 $y$ 轴于 $G$ 点，
$GD=GD'$，$EF=E'F$，$\left(DG+GF+EF+ED\right)_{最小}=D'E'+DE$，
由 $E$ 点坐标为 $\left(5,2\right)$，$D\left(4,4\right)$，
得 $D'\left(-4,4\right)$，$E'\left(5,-2\right)$．
由勾股定理，得
$DE=\sqrt{2^2+1^2} =\sqrt5$，
$D'E'=\sqrt{\left(5+4\right)^2+\left(4+2\right)^2} =\sqrt{117}$，
$\left(DG+GF+EF+ED\right)_{最小}=D'E'+DE= \sqrt{117}+\sqrt5$． -
抛物线上是否在点 $P$，使 $\triangle ODP$ 的面积为 $12$？若存在，求出点 $P$ 的坐标；若不存在，请说明理由．标注答案$\left(\dfrac{29-\sqrt{41}}{8} ,\dfrac{-19-\sqrt{41}}{8} \right)$ 或 $\left( \dfrac{29+\sqrt{41}}{8},\dfrac{-19+\sqrt{41}}{8} \right)$ 或 $\left(\dfrac{29-\sqrt{1001}}{8} , \dfrac{77-\sqrt{1001}}{8}\right)$ 或 $P_4\left(\dfrac{29+\sqrt{1001}}{8} ,\dfrac{77+\sqrt{1001}}{8} \right)$解析因为 $S_{\triangle ODP}=12$，而 $OD=\sqrt{AO^2+AD^2}=4\sqrt2 $．
所以点 $P$ 到 $OD$ 的距离为 $\dfrac{2S_{\triangle OPD}}{OD}=3\sqrt2$．
过点 $O$ 作 $OH\perp OD$，使得 $OH=3\sqrt2$．
① 如图，当点 $H$ 在 $x$ 轴下方时，过点 $H$ 作直线 $HI\parallel OD$，交抛物线与点 $P_1,P_2$．
在 $\mathrm {Rt}\triangle OHI$ 中，$OI=\sqrt 2OH=6$，
所以直线 $HI$ 的解析式为 $y=x-6$．
将 $y=x-6$ 代入 $y=\dfrac45x^2-\dfrac{24}{5}x+4$，
得 $x-6=\dfrac45x^2-\dfrac{24}{5}x+4$，解得 $x_1=\dfrac{29+\sqrt{41}}{8}$，$x_2=\dfrac{29-\sqrt{41}}{8}$，
将 $x_1,x_2$ 的值代入 $y=x-6$，
得 $y_1=\dfrac{-19+\sqrt{41}}{8}$，$y_2=\dfrac{-19-\sqrt{41}}{8}$，
所以点 $P_1\left(\dfrac{29-\sqrt{41}}{8} ,\dfrac{-19-\sqrt{41}}{8} \right)$，$P_2\left( \dfrac{29+\sqrt{41}}{8},\dfrac{-19+\sqrt{41}}{8} \right)$．
② 如图，当点 $H$ 在 $x$ 轴上方时，过点 $H$ 作直线 $HI\parallel OD$，交抛物线与 $P_3$，$P_4$．
在 $\mathrm {Rt}\triangle OHI$ 中，$OI=\sqrt 2OH=6$，
所以直线 $HI$ 的解析式为 $y=x+6$．
将 $y=x+6$ 代入 $y=\dfrac45x^2-\dfrac{24}{5}x+4$，
得 $x+6=\dfrac45x^2-\dfrac{24}{5}x+4$，解得 $x_1=\dfrac{29+\sqrt{1001}}{8}$，$x_2=\dfrac{29-\sqrt{1001}}{8}$．
将 $x_1,x_2$ 的值代入 $y=x+6$，
得 $y_1=x_1+6=\dfrac{77+\sqrt{1001}}{8}$，$y_2=x_2+6=\dfrac{77-\sqrt{1001}}{8} $，
所以 $P_3\left(\dfrac{29-\sqrt{1001}}{8} , \dfrac{77-\sqrt{1001}}{8}\right)$，$P_4\left(\dfrac{29+\sqrt{1001}}{8},\dfrac{77+\sqrt{1001}}{8} \right)$．
综上所述，点 $P$ 的坐标为 $\left(\dfrac{29-\sqrt{41}}{8} ,\dfrac{-19-\sqrt{41}}{8} \right)$，$\left( \dfrac{29+\sqrt{41}}{8},\dfrac{-19+\sqrt{41}}{8} \right)$，$\left(\dfrac{29-\sqrt{1001}}{8},\dfrac{77-\sqrt{1001}}{8}\right)$ 或 $\left(\dfrac{29+\sqrt{1001}}{8} ,\dfrac{77+\sqrt{1001}}{8} \right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
