如图，锐角 $\triangle ABC$ 的外心为 $O$，直线 $BO$ 和 $CO$ 分别与边 $AC,AB$ 交于点 $B',C'$，直线 $B'C'$ 交 $\triangle ABC$ 的外接圆于点 $P,Q$，且 $AP=AQ$．
求证：$\triangle ABC$ 是等腰三角形．
求证：$\triangle ABC$ 是等腰三角形．【难度】
【出处】
2008年全国高中数学联赛辽宁省预赛
【标注】
【答案】
略
【解析】
因为 $AP=AQ$，所以 $\angle APQ=\angle AQP.$ 连接 $BP,QC$ 则$$\angle PBA=\angle AQP=\angle APC'.$$又因为 $\angle PAB$ 为公共角，所以$$\triangle APC' \backsim \triangle ABP,$$则 $AC'\cdot AB={AP}^2$．同理 $AB'\cdot AC={AQ}^2$．又因为 $AP=AQ$，所以 $AC'\cdot AB=AB'\cdot AC$，故 $C',B',C,B$ 共圆，则 $\angle ABO=\angle ACO.$ 连接 $AO$，可知等腰 $\triangle ABO$ 和等腰 $\triangle ACO$ 全等，因此 $AB=AC$，即 $\triangle ABC$ 是等腰三角形．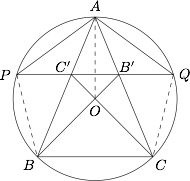
答案
解析
备注
