如图，已知抛物线 $y=-\dfrac{1}{m}\left(x+2\right)\left(x-m\right)(m>0)$ 与 $x$ 轴相交于点 $A,B$，与 $y$ 轴相交于点 $C$，且点 $A$ 在点 $B$ 的左侧．
【难度】
【出处】
无
【标注】
-
若抛物线过点 $G(2,2)$，在抛物线的对称轴上找一点 $H$，使 $AH+CH$ 最小，并求出点 $H$ 的坐标；标注答案$H\left(1, \dfrac32\right)$解析把点 $G$ 坐标代入抛物线解析式，得 $m=4$，
所以抛物线解析式为 $y=-\dfrac14 \left(x+2\right)\left(x-4\right)$，其对称轴为 $x=1$．
如图，连接 $BC$ 交对称轴于点 $H$．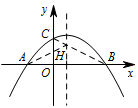
此时 $AH+CH=BH+CH=BC$ 最小．
设直线 $BC$ 的解析式为 $y=kx+b$，
把点 $B,C$ 的坐标代入得 $\begin{cases}4k+b=0,\\b=2,\end{cases}$ 解得 $\begin{cases}k=-\dfrac12,\\b=2.\end{cases}$
所以直线 $BC$ 解析式为 $y=- \dfrac12x+2$，
令 $x=1$，得到 $y=\dfrac32 $，即点 $H\left(1, \dfrac32\right)$． -
在第四象限内，抛物线上是否存在点 $M$，使得以点 $A,B,M$ 为顶点的三角形与 $\triangle ACB$ 相似？若存在，求 $m$ 的值；若不存在，请说明理由．标注答案$m=2\sqrt2 +2$解析在第四象限内，抛物线上存在点 $M$，使得以点 $A$，$B$，$M$ 为顶点的三角形与 $\triangle ACB$ 相似，分两种情况考虑：
① 当 $\triangle ACB\backsim \triangle ABM$ 时，则有 $\dfrac{AC}{AB} =\dfrac{AB}{AM} $，即 $AB^2=AC\cdot AM$，
因为点 $A\left(-2,0\right),C\left(0,2\right)$，即 $OA=OC=2$，
所以 $\angle CAB=45^\circ $，$\angle BAM=45^\circ $，
如图，过 $M$ 作 $MN\perp x$ 轴，交 $x$ 轴于点 $N$，则 $AN=MN$，
所以 $OA+ON=2+ON=MN$．
设 $M\left(x,-x-2\right)$（$x>0$），
把 $M$ 坐标代入抛物线解析式得 $-x-2=-\dfrac{1}{m} \left(x+2\right)\left(x-m\right)$，
因为 $ x>0$，所以 $x+2>0$．
因为 $ m>0$，所以 $ x=2m$，即 $M\left(2m,-2m-2\right)$，
所以 $ AM=\sqrt{\left(2m+2\right)^2+\left(-2m-2\right)^2} =2 \sqrt2\left(m+1\right)$，
因为 $ AB^2=AC\cdot AM$，$AC=2\sqrt2 $，$AB=m+2$，
所以 $\left(m+2\right)^2=2\sqrt2 \cdot 2\sqrt2 \left(m+1\right)$．解得 $m=2\pm 2\sqrt2 $．
因为 $ m>0$，
所以 $ m=2+2\sqrt2 $；
② 当 $\triangle ACB\backsim \triangle MBA$ 时，则 $\dfrac{AB}{MA}= \dfrac{CB}{BA}$，即 $AB^2=CB\cdot MA$．
因为 $\angle CBA=\angle BAM$，$\angle ANM=\angle BOC=90^\circ $，
所以 $ \triangle ANM\backsim \triangle BOC$，所以 $\dfrac{NM}{AN}=\dfrac{OC}{BO} $．
因为 $ OB=m$，设 $ON=x$，所以 $\dfrac{NM}{2+x} =\dfrac{2}{m}$，即 $MN=\dfrac{2}{m} \left(x+2\right)$．
令 $M\left(x,- \dfrac{2}{m}\left(x+2\right)\right)$（$x>0$），
把 $M$ 坐标代入抛物线解析式得 $-\dfrac{2}{m} \left(x+2\right)=-\dfrac{1}{m}\left(x+2\right)\left(x-m\right)$．
因为 $ x>0$，所以 $ x+2>0$．
因为 $ m>0$，所以 $ x=m+2$，即 $M\left(m+2,- \dfrac{2}{m}\left(m+4\right)\right)$．
因为 $AB^2=CB\cdot MA$，$CB= \sqrt{m^2+4}$，$AN=m+4$，$MN=\dfrac{2}{m} \left(m+4\right)$，
所以 $ \left(m+2\right)^2=\sqrt{m^2+4}\cdot\sqrt{\left(m+4\right)^2+\dfrac{4\left(m+4\right)^2}{m^2}} $．整理得 $16=0$，显然不成立，
综上，在第四象限内，当 $m=2\sqrt2 +2$ 时，抛物线上存在点 $M$，使得以点 $A$，$B$，$M$ 为顶点的三角形与 $\triangle ACB$ 相似．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
