如图，在平面直角坐标系中，抛物线 $y=ax^2+bx+c$ 与 $\odot M$ 相交于 $A,B,C,D$ 四点．其中 $A,B$ 两点的坐标分别为 $\left(-1,0\right),\left(0,-2\right)$，点 $D$ 在 $x$ 轴上且 $AD$ 为 $\odot M$ 的直径．点 $E$ 是 $\odot M$ 与 $y$ 轴的另一个交点，过劣弧 $\overparen{ED}$ 上的点 $F$ 作 $FH\perp AD$ 于点 $H$，且 $FH=1.5$．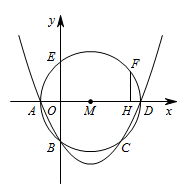
【难度】
【出处】
无
【标注】
-
若点 $ P $ 是 $x$ 轴上的一个动点，试求出 $ \triangle PEF $ 的周长最小时点 $ P $ 的坐标；标注答案$P\left(2,0\right)$解析因为 $ A\left(-1,0\right),B\left(0,-2\right)$，
所以 $ OE=OB=2$，$OA=1$．
因为 $AD$ 是 $\odot M$ 的直径，
所以 $OE\cdot OB=OA\cdot OD$，
即 $2^{2} =1\cdot OD$，$OD=4$，
所以 $ D\left(4,0\right)$．
把 $A\left(-1,0\right),B\left(0,-2\right),D\left(4,0\right)$ 代入 $y = a{x^2} + bx + c$ 得
$ \begin{cases}a - b + c = 0,\\c = - 2,\\ 16a + 4b + c = 0,\end{cases} $ 即 $ \begin{cases}a = \dfrac{1}{2}, \\b = - \dfrac{3}{2},\\c = - 2,\end{cases} $
该抛物线的表达式为 $y = \dfrac{1}{2}{x^2} - \dfrac{3}{2}x - 2$．
连接 $OF$．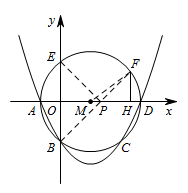
因为 $MF=\dfrac 12 AD=\dfrac 52$，
所以在 $\mathrm {Rt}\triangle MHF$ 中，$MH=\sqrt{MF^2-FH^2}=2$．
而 $OM=MA-OA=\dfrac 32$，
所以 $OH=\dfrac 72$．
所以点 $ F\left(\dfrac 72,\dfrac 32\right)$．
因为点 $B,E$ 关于 $x$ 轴对称，则连接 $BF$ 与 $x$ 轴的交点即为所求点 $P$．
可设直线 $BF$ 的解析式为 $y = kx -2$，
则 $\dfrac 72k-2=\dfrac 32$，解得 $k=1$，
所以直线 $BF$ 的解析式为 $y=x-2$，
从而点 $P\left(2,0\right)$． -
在抛物线的对称轴上是否存在点 $ Q $，使 $ \triangle QCM $ 是等腰三角形？如果存在，请直接写出点 $ Q $ 的坐标；如果不存在，请说明理由．标注答案$Q_1\left(\dfrac{3}{2},\dfrac{5}{2}\right)$，$Q_2\left(\dfrac{3}{2},-\dfrac{5}{2}\right)$，$Q_3\left(\dfrac{3}{2},-4\right)$，$Q_4\left(\dfrac{3}{2},-\dfrac{25}{16}\right)$解析如图所示的四种情况：
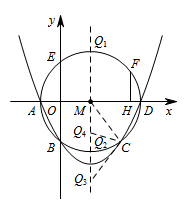
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
