如图，在平面直角坐标系中，抛物线 $y=-\dfrac23x^2-\dfrac43x+2$ 与 $x$ 轴交于 $B,C$ 两点（点 $B$ 在点 $C$ 的左侧），与 $y$ 轴交于点 $A$，抛物线的顶点为 $D$，点 $P$ 是线段 $BC$ 上的动点（点 $P$ 不与点 $B,C$ 重合）．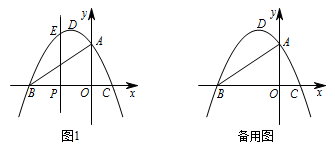
【难度】
【出处】
无
【标注】
-
过点 $P$ 作 $x$ 轴的垂线交抛物线于点 $E$，若 $PE=PC$，求点 $E$ 的坐标；标注答案$\left(-\dfrac32,\dfrac52\right)$解析设点 $P$ 的坐标为 $\left(n,0\right)$．
因为 $ EP\perp x$ 轴，点 $E$ 在抛物线上，
所以点 $E$ 的坐标为 $\left(n,-\dfrac23n^2-\dfrac43n+2\right)$，
因为 $ PE=PC$，
所以 $ -\dfrac23n^2-\dfrac43n+2=1-n$，
所以 $ n_1=-\dfrac32$，$n_2=1$（不符合题意，舍去），
所以 点 $E$ 的坐标为 $\left(-\dfrac32,\dfrac52\right)$． -
在第1问的条件下，点 $F$ 是坐标轴上的点，且点 $F$ 到 $EA$ 和 $ED$ 的距离相等，求线段 $EF$ 的长；标注答案$EF=\dfrac 52$ 或 $\dfrac 32$解析由 $y=-\dfrac 23x^2-\dfrac 43x+2=-\dfrac 23(x+1)^2+\dfrac 83$，
可得点 $A$ 坐标为 $(0,2)$，点 $D$ 坐标为 $\left(-1,\dfrac 83\right)$．
从而可得直线 $AE$ 解析式为 $y=-\dfrac 13x+2$，
直线 $DE$ 解析式为 $y=\dfrac 13x+3$．
设直线 $DE$ 与 $x,y$ 轴分别交于点 $M,N$，直线 $EA$ 与 $x$ 轴交于点 $K$．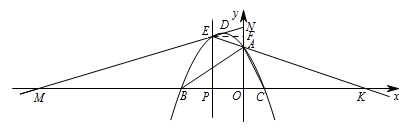
则点 $M(-9,0)$，点 $N(0,3)$，点 $K(6,0)$．
显然 $MP=KP$，
从而得到 $\triangle MEK,\triangle AEN$ 均为等腰三角形．
所以点 $P$ 即为满足条件的点 $F$ 之一，此时 $EF=\dfrac 52$；
过点 $E$ 作 $y$ 轴的垂线，垂足亦为满足条件的点 $F$，此时 $EF=\dfrac 32$．
综上可得，$EF=\dfrac 52$ 或 $\dfrac 32$． -
若点 $Q$ 是线段 $AB$ 上的动点（点 $Q$ 不与点 $A,B$ 重合），点 $R$ 是线段 $AC$ 上的动点（点 $R$ 不与点 $A,C$ 重合），求 $\triangle PQR$ 周长的最小值．标注答案$\dfrac {32\sqrt {65}}{65}$解析如图，假定点 $P$ 固定，作点 $P$ 关于 $AB,AC$ 的对称点 $P_1,P_2$，连接 $P_1P_2$，分别交 $AB,AC$ 于点 $Q,R$，此时 $\triangle PQR$ 的周长最小，最小值即为 $P_1P_2$ 的长度．
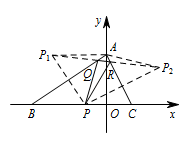连接 $AP_1,AP_2$，则 $AP_1=AP_2=AP$，$\angle P_1AP_2=2\angle BAC$．
故 $\triangle P_1AP_2$ 为顶角固定的等腰三角形，
所以当腰 $AP_1$ 最小时，底边 $P_1P_2$ 取最小值，
而当点 $P$ 与点 $O$ 重合时，$AP$ 取值最小，即此时 $\triangle PQR$ 的周长最小．
如图，分别过 $P_1,P_2$ 作 $x$ 轴的垂线，垂足为点 $S,T$．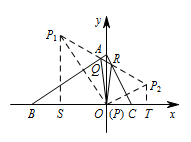
易证 $\triangle OSP_1\backsim \triangle AOB$，
所以 $\dfrac{OS}{OA}=\dfrac{P_1S}{BO}=\dfrac{OP_1}{AB}$．
由抛物线解析式可得 $A\left(0,2\right)$，$B\left(-3,0\right)$，$C\left(1,0\right)$，
所以 $AB=\sqrt{13}$．
而 $OA\cdot OB=\dfrac 12OP_1\cdot AB$，
所以 $OP_1=\dfrac{12\sqrt{13}}{13}$．
所以 $\dfrac{OS}{2}=\dfrac{P_1S}{3}=\dfrac{\dfrac{12\sqrt{13}}{13}}{\sqrt{13}}$，
从而 $OS=\dfrac{24}{13}$，$P_1S=\dfrac{36}{13}$，即点 $P_1\left(-\dfrac{24}{13},\dfrac{36}{13}\right)$．
同理求得点 $F\left(\dfrac 85,\dfrac 45\right)$，
所以此时 $P_1P_2=\dfrac {32\sqrt {65}}{65}$，
即 $\triangle PQR$ 周长的最小值为 $\dfrac {32\sqrt {65}}{65}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
