已知抛物线 $y=- mx^2+4x+2m$ 与 $x$ 轴交于点 $A\left(\alpha ,0\right)$，$B\left(\beta ,0\right)$，且 $\dfrac{1}{\alpha }+\dfrac{1}{\beta }=-2$．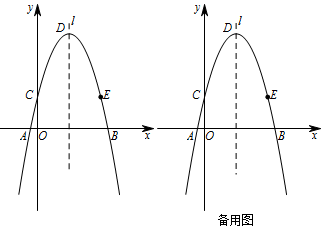
【难度】
【出处】
无
【标注】
-
抛物线的对称轴为 $l$，与 $y$ 轴的交点为 $C$，顶点为 $D$，点 $C$ 关于 $ l $ 对称点为 $E$．是否存在 $x$ 轴上的点 $M$，$y$ 轴上的点 $N$，使四边形 $DNME$ 的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．标注答案$10+2\sqrt 5$解析由题意可知，$\alpha $，$\beta $ 是方程 $ - m{x^2} + 4x + 2m = 0$ 的两根，
由根与系数的关系可得 $\alpha +\beta =\dfrac{4}{m}$，$\alpha \beta =-2$．
因为 $ \dfrac{1}{\alpha } + \dfrac{1}{\beta } = - 2$，
所以 $ \dfrac{\alpha + \beta }{\alpha \beta } = - 2$．即 $\dfrac{{\dfrac{4}{m}}}{ - 2} = - 2$．
所以 $ m=1$．
所以 抛物线解析式为 $y= - {x^2} + 4x + 2$．
存在 $x$ 轴，$y$ 轴上的点 $M$，$N$，使得四边形 $DNME$ 的周长最小．
因为 $ y = - {x^2} + 4x + 2 = - {\left(x - 2\right)^2} + 6$，
所以抛物线的对称轴 $l$ 为 $x = 2$，顶点 $D$ 的坐标为 $\left(2,6\right)$．
又抛物线与 $y$ 轴交点 $C$ 的坐标为 $\left(0,2\right)$，点 $E$ 与点 $C$ 关于 $l$ 对称，
所以 $E$ 点坐标为 $\left(4,2\right)$．
作点 $ D$ 关于 $y$ 轴的对称点 $D'$，作点 $E$ 关于 $x$ 轴的对称点 $E'$，
此时，四边形 $DNME$ 的周长最小为 $D'E'+DE$．（如图所示）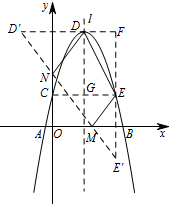
延长 $E'E$，$D'D$ 交于一点 $F$，在 $\mathrm {Rt}\triangle D'E'F$ 中，$D'F=6$，$E'F=8$．
所以 $D'E'=\sqrt {D'{F^2} + E'{F^2}} =\sqrt {{6^2} + {8^2}} = 10$．
设对称轴 $l$ 与 $CE$ 交于点 $G$，在 $\mathrm {Rt}\triangle DGE$ 中，$DG=4$，$EG=2$．
所以 $ DE=\sqrt {D{G^2} + E{G^2}} =\sqrt {{4^2} + {2^2}} = 2\sqrt 5 $．
所以 四边形 $DNME$ 的周长的最小值为 $10+2\sqrt 5$． -
若点 $P$ 在抛物线上，点 $Q$ 在 $x$ 轴上，当以点 $D$，$E$，$P$，$Q$ 为顶点的四边形为平行四边形时，求点 $P$ 的坐标．标注答案点 $P$ 的坐标为 $\left(2 - \sqrt 2 ,4\right)$，$\left(2 + \sqrt 2 ,4\right)$，$\left(2 - \sqrt {10} ,-4\right)$，$\left(2 + \sqrt {10} ,-4\right)$解析如图，$P$ 为抛物线上的点，过 $P$ 作 $PH\perp x$ 轴，垂足为 $H$．
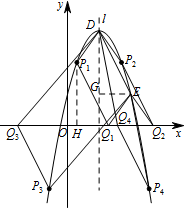若以点 $D$，$E$，$P$，$Q$ 为顶点的四边形为平行四边形，则 $\triangle PHQ\cong \triangle DGE$．
所以 $ PH=DG=4$，即 $\left| y \right| =4$．
所以当 $y=4$ 时，$- {x^2} + 4x + 2 =4$，解得 $x = 2 \pm \sqrt 2 $．
当 $y=-4$ 时，$ - {x^2} + 4x + 2=-4$，解得 $x = 2 \pm \sqrt {10} $．
所以点 $P$ 的坐标为 $\left(2 - \sqrt 2 ,4\right)$，$\left(2 + \sqrt 2 ,4\right)$，$\left(2 - \sqrt {10} ,-4\right)$，$\left(2 + \sqrt {10} ,-4\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
